题目内容
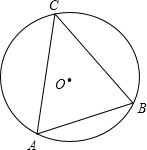（2012•大兴区二模）如图，⊙O的半径为6，点A、B、C在⊙O上，且∠ACB=45°，则弦AB的长是6
| 2 |
6
．| 2 |
分析：连接OA，OB，可以证得△AOB是等腰直角三角形，利用勾股定理即可求解．
解答：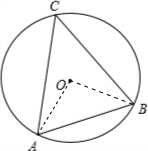
解：连接OA，OB，
∠AOB=2∠ACB=2×45°=90°，
则AB=
=
=6
．
解：连接OA，OB，∠AOB=2∠ACB=2×45°=90°，
则AB=
| OA2+OB2 |
| 62+62 |
| 2 |
点评：本题考查了圆周角定理以及勾股定理，正确证明△AOB是等腰直角三角形是关键．
练习册系列答案
相关题目
（2012•大兴区二模）已知二次函数y=ax2+bx+2，它的图象经过点（1，2）．