题目内容
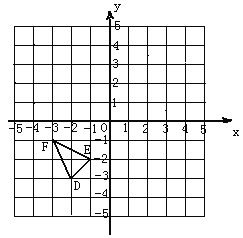
【题目】如图,在正方形网格中,△DEF的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△DEF向右平移5个单位长度,画出平移后的△D1E1F1;
(2) 将△DEF向上平移5个单位长度,再向右平移4个单位长度,画出平移后的△D2E2F2;
(3)求出三角形DEF的面积.
【答案】(1)作图见解析;(2)作图见解析;(3)1.5.
【解析】
(1)分别将三角形的各点向右平移5个单位,然后顺次连接可得出△D1E1F1;
(2)分别将三角形的各点向上平移5个单位,再向右平移4个单位,然后顺次连接可得出△D2E2F2;
(3)运用割补法求△DEF的面积即可.
(1)如图所示,△D1E1F1即为所求作;
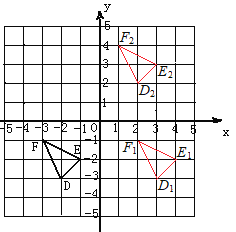
(2)如图所示,△D2E2F2即为所求作;
(3)三角形DEF的面积=2×2-![]() =1.5.
=1.5.

练习册系列答案
相关题目
【题目】为了参加“醴陵市中小学生首届诗词大会”,某中学八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77 ,92, 85;八(2)班79 ,85 ,92,85 ,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | d |
八(2) | a | 85 | 85 | e |
(1)直接写出表中a,b,c的值:a= ,b= ,c= .
(2)求d,e的值,并根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
(3)若“醴陵市中小学生首届诗词大会”中,各中学代表队成绩计分分两部分:现场评委记分和网络评委投票记分。且现场评委记分权数为80%,网络评委投票记分权数为20%,请计算A,B,C三所中学代表队的最终得分为多少?
中学A | 中学B | 中学C | |
评委记分 | 90 | 80 | 85 |
网络投票记分 | 85 | 92 | 88 |