Question

【题目】如图，在菱形ABCD中，AB=2，∠ABC=60°，对角线AC、BD相交于点O，将对角线AC所在的直线绕点O顺时针旋转角α（0°＜α＜90°）后得直线l，直线l与AD、BC两边分别相交于点E和点F．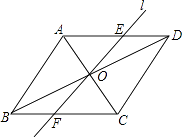

（1）求证：△AOE≌△COF；
（2）当α=30°时，求线段EF的长度．

Answer 1

【答案】
（1）解：∵四边形ABCD是菱形，

∴AD∥BC，AO=OC，

∴ ，

∴AE=CF，OE=OF，

在△AOE和△COF中，

∴△AOE≌△COF．

（2）解：当α=30°时，即∠AOE=30°，

∵四边形ABCD是菱形，∠ABC=60°，

∴∠OAD=60°，

∴∠AEO=90°，

在Rt△AOB中，

sin∠ABO= = = ，

∴AO=1，

在Rt△AEO中，

cos∠AOE=cos30°= = ，

∴OE= ，

∴EF=2OE= ．

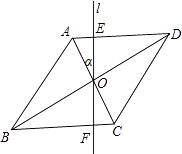
【解析】（1）首先证明AE=CF，OE=OF，结合AO=CO，利用SSS证明△AOE≌△COF；（2）首先画出α=30°时的图形，根据菱形的性质得到EF⊥AD，解三角形即可求出OE的长，进而得到EF的长．