题目内容
如图，某电信公司计划修建一条连接B、C两地的电缆。测量人员在山脚A点测得B、C两地的仰角分别为30°、45°，在B处测得C地的仰角为60°，已知C地比A地高200m。求电缆BC的长（结果保留根号）.
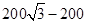
解：画BE、CF均垂直于AM，垂足分别为E、F；画BD⊥CF于D.
则四边形BEFD是矩形. 设BD=x，由题意得
AF=CF=200，EF=BD=x,AE=200－ x
∵∠CBD=60°，
∴CD=tan60°·BD=
x，BE=DF=200－x
∵
=" tan∠BAE=" tan30°=
，
即
=,
解得x =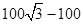
，
∴BC=2x=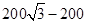 （m）
则四边形BEFD是矩形. 设BD=x，由题意得
AF=CF=200，EF=BD=x,AE=200－ x
∵∠CBD=60°，
∴CD=tan60°·BD=
x，BE=DF=200－x∵
=" tan∠BAE=" tan30°=，即
=,解得x =
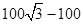，∴BC=2x=
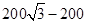（m）
练习册系列答案
相关题目
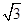，堤高BC=5m，则坡面AB的长度是．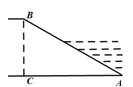
．
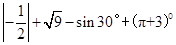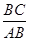
米的点P处．这时，一辆出租车由西向东匀速行驶，测得此车从A处行驶到B处所用的时间为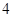
秒且∠APO=60°，∠BPO =45°． 
，
）
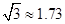