题目内容
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线. 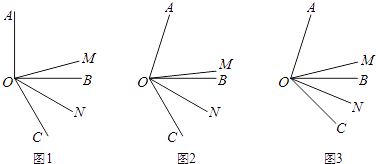
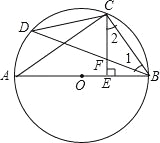
(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
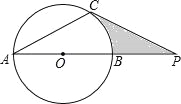
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON=(直接写出结果).
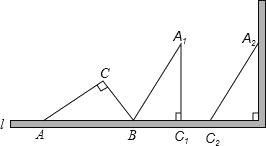
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON=(直接写出结果).
【答案】
(1)解:如图1,∵∠AOB=90°,∠BOC=60°,
∴∠AOC=90°+60°=150°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC= ![]() ∠AOC=75°,∠NOC=
∠AOC=75°,∠NOC= ![]() ∠BOC=30°
∠BOC=30°
∴∠MON=∠MOC﹣∠NOC=45°
(2)35°
(3)![]() α
α
【解析】解:(2)如图2, ∵∠AOB=70°,∠BOC=60°,
∴∠AOC=70°+60°=130°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC= ![]() ∠AOC=65°,∠NOC=
∠AOC=65°,∠NOC= ![]() ∠BOC=30°
∠BOC=30°
∴∠MON=∠MOC﹣∠NOC=65°﹣30°=35°.
所以答案是:35°.(3)如图3,∠MON= ![]() α,与β的大小无关.
α,与β的大小无关.
理由:∵∠AOB=α,∠BOC=β,
∴∠AOC=α+β.
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC= ![]() ∠AOC=
∠AOC= ![]() (α+β),
(α+β),
∠NOC= ![]() ∠BOC=
∠BOC= ![]() β,
β,
∴∠AON=∠AOC﹣∠NOC=α+β﹣ ![]() β=α+
β=α+ ![]() β.
β.
∴∠MON=∠MOC﹣∠NOC
= ![]() (α+β)﹣
(α+β)﹣ ![]() β=
β= ![]() α
α
即∠MON= ![]() α.
α.
所以答案是: ![]() α.
α.
【考点精析】掌握角的平分线和角的运算是解答本题的根本,需要知道从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目