题目内容
【题目】(12分)如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
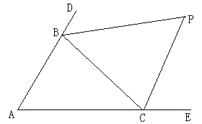
(1)若∠A=50°,则∠P= °;
(2)若∠A=90°,则∠P= °;
(3)若∠A=100°,则∠P= °;
(4)请你用数学表达式归纳∠A与∠P的关系,并说明理由。
【答案】解:(1)∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,∠DBC+∠BCE=360°-130°=230°,
又∵∠CBD与∠BCE的平分线相交于点P,
∴∠PBC=![]() ∠DBC,∠PCB=
∠DBC,∠PCB=![]() ∠ECB,
∠ECB,
∴∠PBC+∠PCB=![]() (∠DBC+∠ECB)=115°,
(∠DBC+∠ECB)=115°,
∴∠P=65°.
同理得:(2)45°;
(3)40°
(4)∠P=90°-![]() ∠A.理由如下:
∠A.理由如下:
∵BP平分∠DBC,CP平分∠BCE,
∴∠DBC=2∠CBP,∠BCE=2∠BCP
又∵∠DBC=∠A+∠ACB∠BCE=∠A+∠ABC,
∴2∠CBP=∠A+∠ACB,2∠BCP=∠A+∠ABC,
∴2∠CBP+2∠BCP=∠A+∠ACB+∠A+∠ABC=180°+∠A,
∴∠CBP+∠BCP=90°+![]() ∠A
∠A
又∵∠CBP+∠BCP+∠P=180°,
∴∠P=90°-![]() ∠A.
∠A.
【解析】试题分析:(1)若∠A=50°,则有∠ABC+∠ACB=130°,∠DBC+∠BCE=360°-130°=230°,根据角平分线的定义可以求得∠PBC+∠PCB的度数,再利用三角形的内角和定理即可求得∠P的度数;
(2)、(3)和(1)的解题步骤类似;(4)利用角平分线的性质和三角形的外角性质可求出∠BCP=![]() (∠A+∠ABC),∠CBP=
(∠A+∠ABC),∠CBP=![]() (∠A+∠ACB);再利用三角形内角和定理即可求出∠A与∠P的关系.
(∠A+∠ACB);再利用三角形内角和定理即可求出∠A与∠P的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目