题目内容
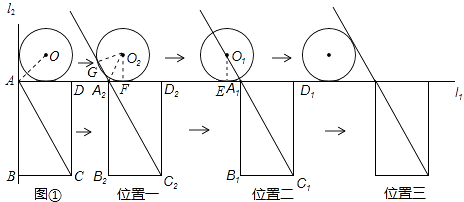
【题目】如图,已知l1⊥l2 , ⊙O与l1 , l2都相切,⊙O的半径为2cm,矩形ABCD的边AD、AB分别与l1 , l2重合,AB=4 ![]() cm,AD=4cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s)
cm,AD=4cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s) 
(1)如图①,连接OA、AC,则∠OAC的度数为°;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1 , A1 , C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm),当d<2时,求t的取值范围(解答时可以利用备用图画出相关示意图).
【答案】
(1)105
(2)解:
如图位置二,当O1,A1,C1恰好在同一直线上时,设⊙O1与l1的切点为E,
连接O1E,可得O1E=2,O1E⊥l1,
在Rt△A1D1C1中,∵A1D1=4,C1D1=4 ![]() ,
,
∴tan∠C1A1D1= ![]() ,∴∠C1A1D1=60°,
,∴∠C1A1D1=60°,
在Rt△A1O1E中,∠O1A1E=∠C1A1D1=60°,
∴A1E= ![]() =
= ![]() ,
,
∵A1E=AA1﹣OO1﹣2=t﹣2,
∴t﹣2= ![]() ,
,
∴t= ![]() +2,
+2,
∴OO1=3t=2 ![]() +6
+6
(3)解:

①当直线AC与⊙O第一次相切时,设移动时间为t1,
如图位置一,此时⊙O移动到⊙O2的位置,矩形ABCD移动到A2B2C2D2的位置,
设⊙O2与直线l1,A2C2分别相切于点F,G,连接O2F,O2G,O2A2,
∴O2F⊥l1,O2G⊥A2C2,
由(2)得,∠C2A2D2=60°,∴∠GA2F=120°,
∴∠O2A2F=60°,
在Rt△A2O2F中,O2F=2,∴A2F= ![]() ,
,
∵OO2=3t1,AF=AA2+A2F=4t1+ ![]() ,
,
∴4t1+ ![]() ﹣3t1=2,
﹣3t1=2,
∴t1=2﹣ ![]() ,
,
②当直线AC与⊙O第二次相切时,设移动时间为t2,
记第一次相切时为位置一,点O1,A1,C1共线时位置二,第二次相切时为位置三,
由题意知,从位置一到位置二所用时间与位置二到位置三所用时间相等,
∴ ![]() +2﹣(2﹣
+2﹣(2﹣ ![]() )=t2﹣(
)=t2﹣( ![]() +2),
+2),
解得:t2=2+2 ![]() ,
,
综上所述,当d<2时,t的取值范围是:2﹣ ![]() <t<2+2
<t<2+2 ![]()
【解析】解:(1)∵l1⊥l2 , ⊙O与l1 , l2都相切, ∴∠OAD=45°,
∵AB=4 ![]() cm,AD=4cm,
cm,AD=4cm,
∴CD=4 ![]() cm,
cm,
∴tan∠DAC= ![]() =
= ![]() =
= ![]() ,
,
∴∠DAC=60°,
∴∠OAC的度数为:∠OAD+∠DAC=105°,
故答案为:105;
(1)利用切线的性质以及锐角三角函数关系分别求出∠OAD=45°,∠DAC=60°,进而得出答案;(2)首先得出,∠C1A1D1=60°,再利用A1E=AA1﹣OO1﹣2=t﹣2,求出t的值,进而得出OO1=3t得出答案即可;(3)①当直线AC与⊙O第一次相切时,设移动时间为t1 , ②当直线AC与⊙O第二次相切时,设移动时间为t2 , 分别求出即可.

 名校课堂系列答案
名校课堂系列答案


