题目内容
已知,点P(x,y)在第一象限,且点P(x,y)在直线l:x+y=12的图象上,点A(10,0)在x轴上,设△OPA的面积为S.
(1)求S关于x的关系式,并确定x的取值范围;
(2)画出S关于x的函数图象;
(3)在直线l上是否存在点M使△OAM是等腰三角形?若存在,求出点M的个数.

(1)求S关于x的关系式,并确定x的取值范围;
(2)画出S关于x的函数图象;
(3)在直线l上是否存在点M使△OAM是等腰三角形?若存在,求出点M的个数.

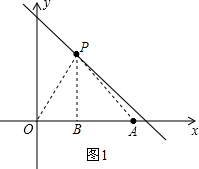
(1)如图1所示:
过点P作PB⊥x轴,连接OP,AP,
∵由点P(x,y)在直线l:x+y=12的图象上,
∴y=12-x,
∴S=
×OA×PB=
×10×(12-x)=60-5x(0<x<12);
(2)∵由(1)可知,S=60-5x,
∴当x=0时,S=60,当S=0时,x=12,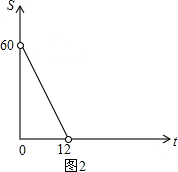
∴S与x的函数图象如图2所示:
(3)存在.
设点M(m,12-m),
当OM=OA时,m2+(12-m)2=100,解得m1=6+
,m2=6-
,
故此时M(6+
,6-
)或(6-
,6+
);
当OA=AM时,100=(m-10)2+(12-m)2,解得m1=18,m2=4,
故此时M(18,-6)或(4,8);
当OM=AM时,m2+(12-m)2=(m-10)2+(12-m)2,解得m=5,
故此时M(5,7).
综上所述,M点的坐标为M(6+
,6-
),(6-
,6+
),(18,-6),(4,8),(5,7).
过点P作PB⊥x轴,连接OP,AP,
∵由点P(x,y)在直线l:x+y=12的图象上,
∴y=12-x,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵由(1)可知,S=60-5x,
∴当x=0时,S=60,当S=0时,x=12,

∴S与x的函数图象如图2所示:
(3)存在.
设点M(m,12-m),
当OM=OA时,m2+(12-m)2=100,解得m1=6+
| 14 |
| 14 |
故此时M(6+
| 14 |
| 14 |
| 14 |
| 14 |
当OA=AM时,100=(m-10)2+(12-m)2,解得m1=18,m2=4,
故此时M(18,-6)或(4,8);
当OM=AM时,m2+(12-m)2=(m-10)2+(12-m)2,解得m=5,
故此时M(5,7).
综上所述,M点的坐标为M(6+
| 14 |
| 14 |
| 14 |
| 14 |


练习册系列答案
相关题目
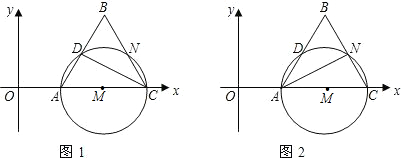 满足条件的点P的坐标;若不存在,请说明理由.(图2为备用图)
满足条件的点P的坐标;若不存在,请说明理由.(图2为备用图) 坐标系(如图).
坐标系(如图).









 度)与应付电费y(元)的关系如图所示.
度)与应付电费y(元)的关系如图所示.