题目内容
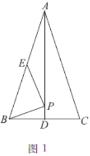
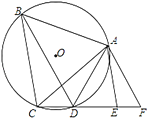
【题目】如图,已知![]() 是等边三角形
是等边三角形![]() 的外接圆,点
的外接圆,点![]() 在圆上,在
在圆上,在![]() 的延长线上有一点
的延长线上有一点![]() ,使
,使![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 是
是![]() 的切线
的切线
(2)若![]() ,求
,求![]() 的长
的长
【答案】(1)证明见解析;(2)6
【解析】
(1)根据等边三角形的性质可得∠OAC=30°,∠BCA=60°,根据平行线的性质得到∠EAC=60°,求出∠OAE=90°,可得AE是⊙O的切线;
(2)先根据等边三角形性质得AB=AC,∠BAC=∠ABC=60°,由四点共圆得∠ADF=∠ABC=60°,得△ADF是等边三角形,然后证明△BAD≌△CAF,可得![]() 的长.
的长.
证明:(1)连接OA,
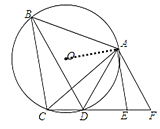
∵⊙O是等边三角形ABC的外接圆,
∴∠OAC=30°,∠BCA=60°,
∵AE∥BC,
∴∠EAC=∠BCA=60°,
∴∠OAE=∠OAC+∠EAC=30°+60°=90°,
∴AE是⊙O的切线;
(2)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ABC=60°,
∵A、B、C、D四点共圆,
∴∠ADF=∠ABC=60°,
∵AD=DF,
∴△ADF是等边三角形,
∴AD=AF,∠DAF=60°,
∴∠BAC+∠CAD=∠DAF+∠CAD,即∠BAD=∠CAF,
在△BAD和△CAF中,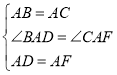 ,
,
∴△BAD≌△CAF,
∴BD=CF=6.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
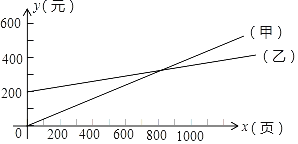
小学生10分钟应用题系列答案【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A |
|
|
B |
|
|
C |
|
|
D |
|
|
E |
|
|
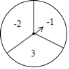
调查结果扇形统计图
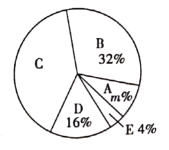
请根据以上图表,解答下列问题:
(1)这次被调查的同学共有______人,![]() ______,
______,![]() _______;
_______;
(2求扇形统计图中C所在的扇形的圆心角度数;.
(3)该校共有学生![]() 人,请估计每月零花钱的数额
人,请估计每月零花钱的数额![]() 在
在![]() 范围内的人数.
范围内的人数.
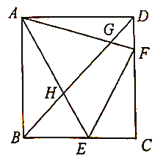
【题目】如图1,在等腰![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() .在线段
.在线段![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,
,![]() .若
.若![]() ,
,![]() ,设
,设![]() (当点
(当点![]() 与点
与点![]() 重合时,
重合时,![]() 的值为0),
的值为0),![]() .
.
小明根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变换而变化的规律进行了探究.
的变换而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)通过取点、画图、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 5.2 | 4.2 | 4.6 | 5.9 | 7.6 | 9.5 |
(说明:补全表格时,相关数值保留一位小数)
(参考数据:![]() ,
,![]() ,
,![]() )
)
(2)建立平面直角坐标系(图2),描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)函数![]() 的最小值为 (保留一位小数),此时点
的最小值为 (保留一位小数),此时点![]() 在图1中的什么位置.
在图1中的什么位置.