题目内容
对于大于或等于2的自然数m的n次幂进行如下方式的“分裂”：
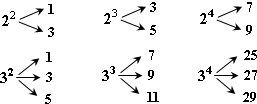
仿上，52的“分裂”中最大的数是 ，若m3的“分裂”中最小数是21，则m= ．
仿上，52的“分裂”中最大的数是
分析：观察题中给出的“分裂”得到52“分裂”为5个从1开始的连续奇数，即1+3+5+7+9，得到最大的数为9；m3“分裂”为m个连续奇数，由于最小数是21，然后依次相加得到21+23=44，44+25=69，69+27=96，96+29=125，即有125=53，所以m=5．
解答：解：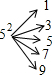
，所以52的“分裂”中最大的数为9；
m3的“分裂”中最小数是21，则接下的数为23、25、…，
∵21+23=44，44+25=69，69+27=96，96+29=125，
而125=53，
∴m=5．
故答案为9，5．
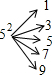，所以52的“分裂”中最大的数为9；m3的“分裂”中最小数是21，则接下的数为23、25、…，
∵21+23=44，44+25=69，69+27=96，96+29=125，
而125=53，
∴m=5．
故答案为9，5．
点评：本题考查了规律型：数字的变化类：通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．
练习册系列答案
名校课堂系列答案
相关题目
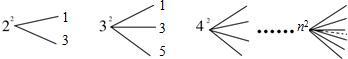12、对于大于或等于2的自然数n的平方进行如下“分裂”，分裂成n个连续奇数的和，则自然数72的分裂数中最大的数是
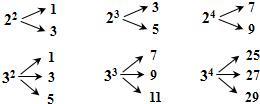9、对于大于或等于2的自然数m的n次幂进行如下方式的“分裂”：仿上，52的“分裂”中最大的数是
