题目内容
【题目】如图,直线![]() 在平面直角坐标系中与
在平面直角坐标系中与![]() 轴交于点A,点B(-3,3)也在直线
轴交于点A,点B(-3,3)也在直线![]() 上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线
上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线![]() 上.
上.
(1)求点C的坐标和直线![]() 的解析式;
的解析式;
(2)已知直线![]() :
:![]() 经过点B,与
经过点B,与![]() 轴交于点E,求△ABE的面积.
轴交于点E,求△ABE的面积.

【答案】(1)C(-2,1),直线![]() 的解析式为
的解析式为![]() .(2)13.5
.(2)13.5
【解析】
试题(1)根据平移的法则即可得出点C的坐标,设直线l1的解析式为y=kx+c,根据点B、C的坐标利用待定系数法即可求出直线l1的解析式;
(2)由点B的坐标利用待定系数法即可求出直线l2的解析式,再根据一次函数图象上点的坐标特征求出点A、E,根据三角形的面积公式即可求出△ABE的面积.
试题解析:(1)由平移法则得:C点坐标为(-3+1,3-2),即(-2,1).
设直线l1的解析式为y=kx+c,
则![]() ,解得:
,解得:![]() ,
,
∴直线l1的解析式为y=-2x-3.
(2)把B点坐标代入y=x+b得,
3=-3+b,解得:b=6,
∴y=x+6.
当x=0时,y=6,
∴点E的坐标为(0,6).
当x=0时,y=-3,
∴点A坐标为(0,-3),
∴AE=6+3=9,
∴△ABE的面积为![]() ×9×|-3|=13.5.
×9×|-3|=13.5.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.
对雾霾了解程度的统计表:
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
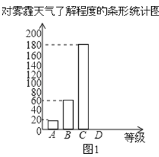
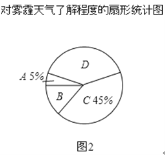
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.