题目内容
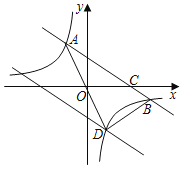
【题目】如图,一次函数y=kx+b(k<0)的图象与反比例函数y=![]() 图象都经过点A(a,4),一次函数y=kx+b(k<0)的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.
图象都经过点A(a,4),一次函数y=kx+b(k<0)的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.
(1)求这两个函数的表达式;
(2)将直线AB向下平移5个单位长度后与第四象限内的反比例函数图象交于点D,连接AD、BD,求△ADB的面积.
【答案】(1)y=﹣![]() x+2,y=﹣
x+2,y=﹣![]() ;(2)
;(2)![]()
【解析】
(1)先由一次函数y=kx+b(k<0)的图象经过点C(3,0),得出3k+b=0①,由于一次函数y=kx+b的图象与y轴的交点是(0,b),根据三角形的面积公式可求得b的值,然后利用待定系数法即可求得函数解析式;
(2)将直线AB向下平移5个单位后得到直线ED的解析式为y=﹣![]() x﹣3,得到E(﹣
x﹣3,得到E(﹣![]() ,0),解方程组得到B(6,﹣2),连接AE,BE,根据三角形的面积公式即可得到结论.
,0),解方程组得到B(6,﹣2),连接AE,BE,根据三角形的面积公式即可得到结论.
解:(1)∵一次函数y=kx+b(k<0)的图象经过点C(3,0),
∴3k+b=0①,点C到y轴的距离是3,
∵k<0,
∴b>0,
∵一次函数y=kx+b的图象与y轴的交点是(0,b),
∴![]() ×3×b=3,
×3×b=3,
解得:b=2.
把b=2代入①,解得:k=﹣![]() ,则函数的解析式是y=﹣
,则函数的解析式是y=﹣![]() x+2.
x+2.
故这个函数的解析式为y=﹣![]() x+2;
x+2;
把点A(a,4)代入y=﹣![]() x+2得,4=﹣
x+2得,4=﹣![]() a+2,
a+2,
解得:a=﹣3,
∴A(﹣3,4),
∴m=﹣12,
∴反比例函数的解析式为y=﹣![]() ;
;
(2)∵将直线AB向下平移5个单位后得到直线ED的解析式为y=﹣![]() x﹣3,
x﹣3,
当y=0时,即0=﹣![]() x﹣3,
x﹣3,
解得:x=﹣![]() ,
,
∴E(﹣![]() ,0),
,0),
解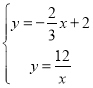 得,
得,![]() ,
,![]() ,
,
∴B(6,﹣2),
连接AE,BE,
∵AB∥DE,
∴S△ADB=S△AEB=![]() (3+
(3+![]() )×4+
)×4+![]() ×(3+
×(3+![]() )×2=
)×2=![]() .
.


【题目】2020年是5G爆发元年,三大运营商都在政策的支持下,加快着5G建设的步伐.某通信公司实行的5G畅想套餐,部分套餐资费标准如下:
套餐类型 | 月费(元/月) | 套餐内包含内容 | 套餐外资费 | ||
国内数据流量(GB) | 国内主叫(分钟) | 国内流量 | 国内主叫 | ||
套餐1 | 128 | 30 | 200 | 每5元1GB,用满3GB后每3元1GB,不足部分按照0.03/元MB收取 | 0.19元/分钟 |
套餐2 | 158 | 40 | 300 | ||
套餐3 | 198 | 60 | 500 | ||
套餐4 | 238 | 80 | 600 | ||
小武每月大约使用国内数据流量49GB,国内主叫350分钟,若想使每月付费最少,则他应预定的套餐是( )
A.套餐1B.套餐2C.套餐3D.套餐4
【题目】自从开展“创建全国文明城区“工作以来,门头沟区便掀起了“门头沟热心人“志愿服务的热潮,区教委也号召各校学生积极参与到志愿服务当中.为了解甲、乙两所学校学生一周志愿服务情况,从这两所学校中各随机抽取40名学生,分别对他们一周的志愿服务时长(单位:分钟)数据进行收集、整理、描述和分析.下面给出了部分信息:
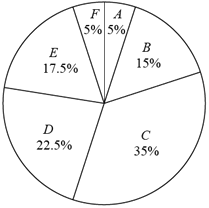
a.甲校40名学生一周的志愿服务时长的扇形统计图如图(数据分成6组:![]() ):
):
A:![]() B:
B:![]()
C:![]() D:
D:![]()
E:![]() F:
F:![]()
b.甲校40名学生一周志愿服务时长在![]() 这一组的是:
这一组的是:
60 60 62 63 65 68 70 72 73 75 75 76 80 80
c.甲、乙两校各抽取的40名学生一周志愿服务时长的平均数、中位数、众数如下:
学校 | 平均数 | 中位数 | 众数 |
甲校 | 75 |
| 90 |
乙校 | 75 | 76 | 85 |
根据以上信息,回答下列问题:
(1)![]() _____________;
_____________;
(2)根据上面的统计结果,你认为____①_____所学校学生志愿服务工作做得好(填“甲“或“乙“),理由______②________________________________________________________;
(3)甲校要求学生一周志愿服务的时长不少于60分钟,如果甲校共有学生800人,请估计甲校学生中一周志愿服务时长符合要求的有_______人.