题目内容
【题目】如图,直线AB、CD相交于点O,∠BOC=80°,OE是∠BOC的角平分线,OF是OE的反向延长线.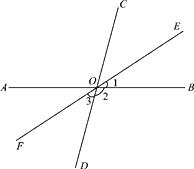
(1)求∠2、∠3的度数;
(2)说明OF平分∠AOD的理由.
【答案】
(1)解:∵∠BOC+∠2=180°,∠BOC=80°,
∴∠2=180°﹣80°=100°;
∵OE是∠BOC的角平分线,
∴∠1=40°.
∵∠1+∠2+∠3=180°,
∴∠3=180°﹣∠1﹣∠2=180°﹣40°﹣100°=40° 。
(2)解:∵∠2+∠3+∠AOF=180°,
∴∠AOF=180°﹣∠2﹣∠3=180°﹣100°﹣40°=40°,
∴∠AOF=∠3=40°,
∴OF平分∠AOD 。
【解析】(1)根据邻补角的定义得出∠2=180°﹣∠BOC=100°;根据角平分线的定义得出∠1=40°.根据平角的定义得出∠3=180°﹣∠1﹣∠2=180°﹣40°﹣100°=40° ;
(2)根据平角的定义得出∠AOF=180°﹣∠2﹣∠3=180°﹣100°﹣40°=40°,根据等量代换得出∠AOF=∠3=40°,从而得出结论OF平分∠AOD 。

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】某水果公司以1.5元/千克的成本新进了20000千克柑橘,销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率”统计,并把获得的数据记录在下表中:
柑橘总质量n/千克 | 损坏柑橘质量m/千克 | 柑橘损坏的频率m/n |
100 | 11.00 | 0.110 |
200 | 21.00 | 0.105 |
300 | 30.30 | |
400 | 38.84 | |
500 | 48.50 | |
600 | 61.86 | |
700 | 70.64 | |
800 | 78.48 | |
900 | 89.14 | |
1000 | 103.08 |
(1)请你完成表格;
(2)如果公司希望这些柑橘能够获得税前利润10000元以上,那么在出售柑橘(已去掉损坏的柑橘)时,大约每千克定价为多少元比较合适?