题目内容
在课堂上,郝老师将一个三角板的直角顶点与点C重合,它的两条直角边也分别与x轴正半轴、y轴正半轴相交于E点、D点.当三角板绕点C旋转到与x轴、y轴垂直时,如图1,已知射线OM为第一象限的角平分线,C点的坐标为(2,2)

(1)四边形ODCE的面积是
(2)当郝老师将三角板绕点C旋转到与x轴、y轴不垂直时,如图2,姚小明同学马上举手回答说,在旋转过程中,四边形ODCE的面积始终保持不变,其值为定值.老师说他的回答是正确的!请你说明其中的道理.
(3)最后,郝老师过D、O、E三点画⊙O1,如图3,设△DOE的内切圆的直径为d,并用肯定的语气说,不论⊙O1的大小、位置如何变化,d+DE的值永远不变.同学们,你们知道这里的奥妙吗?请说明理由.

(1)四边形ODCE的面积是
4
4
;点D的坐标为(0,2)
(0,2)
;点E的坐标为(2,0)
(2,0)
.(2)当郝老师将三角板绕点C旋转到与x轴、y轴不垂直时,如图2,姚小明同学马上举手回答说,在旋转过程中,四边形ODCE的面积始终保持不变,其值为定值.老师说他的回答是正确的!请你说明其中的道理.
(3)最后,郝老师过D、O、E三点画⊙O1,如图3,设△DOE的内切圆的直径为d,并用肯定的语气说,不论⊙O1的大小、位置如何变化,d+DE的值永远不变.同学们,你们知道这里的奥妙吗?请说明理由.
分析:(1)由于DC⊥y轴,CE⊥x轴,OM为第一象限的角平分线,则四边形ODCE为矩形且CD=CE,则四边形ODCE为正方形,由C点坐标为(2,2),易得到四边形ODCE的面积,点D的坐标和点E的坐标;
(2)过C作CF⊥y轴于F,CH⊥x轴于H,与(1)一样可得到四边形OFCE为正方形,其面积为4,再根据等角的余角相等可得到∠FCD=∠HCE,易证得Rt△FCD≌Rt△HCE,则S△FCD=S△HCE,于是得到
S四边形ODCE=S正方形OFCH=4,说明在旋转过程中,四边形ODCE的面积始终保持不变,其值为定值;
(3)过C作CF⊥y轴于F,CH⊥x轴于H,⊙O′分别切OE于K,切OD于P,切DE于Q,根据切线的性质得O′K=O′P,易得四边形OPO′K为正方形,设⊙O′的半径为r,根据切线长定理得到OP=OK=r,EK=EQ=EO-r,DQ=DP=OD-r,利用DQ+EQ=ED得EO-r+OD-r=DE,则DE+2r=OE+OD=OH+HE+OF-DF,根据(2)中得结论得到DF=HE,OH=OF=2,于是有DE+2r=2+2=4,即d+DE=4.
(2)过C作CF⊥y轴于F,CH⊥x轴于H,与(1)一样可得到四边形OFCE为正方形,其面积为4,再根据等角的余角相等可得到∠FCD=∠HCE,易证得Rt△FCD≌Rt△HCE,则S△FCD=S△HCE,于是得到
S四边形ODCE=S正方形OFCH=4,说明在旋转过程中,四边形ODCE的面积始终保持不变,其值为定值;
(3)过C作CF⊥y轴于F,CH⊥x轴于H,⊙O′分别切OE于K,切OD于P,切DE于Q,根据切线的性质得O′K=O′P,易得四边形OPO′K为正方形,设⊙O′的半径为r,根据切线长定理得到OP=OK=r,EK=EQ=EO-r,DQ=DP=OD-r,利用DQ+EQ=ED得EO-r+OD-r=DE,则DE+2r=OE+OD=OH+HE+OF-DF,根据(2)中得结论得到DF=HE,OH=OF=2,于是有DE+2r=2+2=4,即d+DE=4.
解答:解:(1)∵DC⊥y轴,CE⊥x轴,
∴四边形ODCE为矩形,
而C点坐标为(2,2),则C点在第一象限的角平分线OM上,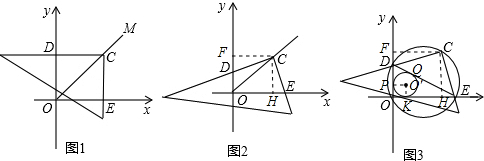
∴四边形ODCE为正方形,且边长为2,
∴四边形ODCE的面积是2×2=4,点D的坐标为(0,2),点E的坐标为(2,0),
故答案为:4,(0,2),(2,0);
(2)过C作CF⊥y轴于F,CH⊥x轴于H,如图2,
则CF=CH=2,
∴四边形OFCH为正方形,其面积为4,
∵∠DCE=90°,∠FCH=90°,
∴∠FCD+∠DCH=90°,∠DCH+∠HCE=90°,
∴∠FCD=∠HCE,
在Rt△FCD和Rt△HCE中
,
∴Rt△FCD≌Rt△HCE,
∴S△FCD=S△HCE,
∴S四边形ODCE=S正方形OFCH=4.
(3)不论⊙O1的大小、位置如何变化,d+DE的值永远不变,如图3.理由如下:
过C作CF⊥y轴于F,CH⊥x轴于H,△DOE的内切圆⊙O′分别切OE于H,切OD于P,切DE于Q,如图3,
∴O′K=O′P,
∴四边形OPO′K为正方形,
设⊙O′的半径为r,则OP=OK=r,EK=EQ=EO-r,DQ=DP=OD-r,
∴EO-r+OD-r=DE,
∴DE+2r=OE+OD=OH+HE+OF-DF,
由(2)得DF=HE,OH=OF=2,
∴DE+2r=2+2=4,
∴d+DE=4,即不论⊙O1的大小、位置如何变化,d+DE的值永远不变.
∴四边形ODCE为矩形,
而C点坐标为(2,2),则C点在第一象限的角平分线OM上,

∴四边形ODCE为正方形,且边长为2,
∴四边形ODCE的面积是2×2=4,点D的坐标为(0,2),点E的坐标为(2,0),
故答案为:4,(0,2),(2,0);
(2)过C作CF⊥y轴于F,CH⊥x轴于H,如图2,
则CF=CH=2,
∴四边形OFCH为正方形,其面积为4,
∵∠DCE=90°,∠FCH=90°,
∴∠FCD+∠DCH=90°,∠DCH+∠HCE=90°,
∴∠FCD=∠HCE,
在Rt△FCD和Rt△HCE中
|
∴Rt△FCD≌Rt△HCE,
∴S△FCD=S△HCE,
∴S四边形ODCE=S正方形OFCH=4.
(3)不论⊙O1的大小、位置如何变化,d+DE的值永远不变,如图3.理由如下:
过C作CF⊥y轴于F,CH⊥x轴于H,△DOE的内切圆⊙O′分别切OE于H,切OD于P,切DE于Q,如图3,
∴O′K=O′P,
∴四边形OPO′K为正方形,
设⊙O′的半径为r,则OP=OK=r,EK=EQ=EO-r,DQ=DP=OD-r,
∴EO-r+OD-r=DE,
∴DE+2r=OE+OD=OH+HE+OF-DF,
由(2)得DF=HE,OH=OF=2,
∴DE+2r=2+2=4,
∴d+DE=4,即不论⊙O1的大小、位置如何变化,d+DE的值永远不变.
点评:本题考查了圆的综合题:圆的切线垂直于过切点的半径;从圆外一点引圆的两条切线,切线长相等;掌握旋转的性质以及三角形全等的判定与性质以及正方形的性质.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 29、实践与操作:在课堂上,李老师和同学们探究了与三角形面积相关的问题.如图,已知点A、B同在直线a上,点C1、C2在直线a的同一侧.
29、实践与操作:在课堂上,李老师和同学们探究了与三角形面积相关的问题.如图,已知点A、B同在直线a上,点C1、C2在直线a的同一侧.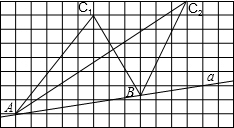 实践与操作:在课堂上,李老师和同学们探究了与三角形面积相关的问题.如图,已知点A、B同在直线a上,点C1、C2在直线a的同一侧.
实践与操作:在课堂上,李老师和同学们探究了与三角形面积相关的问题.如图,已知点A、B同在直线a上,点C1、C2在直线a的同一侧.