题目内容
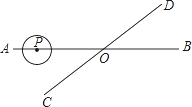
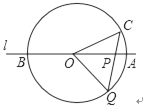
【题目】如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于点Q.是否存在点P,使得QP=QO;若存在,求出相应的∠OCP的大小;若不存在,请简要说明理由.
【答案】40°、20°、100°.
【解析】
点P是直线l上的一个动点,因而点P与线段AO有三种位置关系,在线段AO上,点P在OB上,点P在OA的延长线上.分这三种情况进行讨论即可.
①根据题意,画出图(1),
在△QOC中,OC=OQ,
∴∠OQC=∠OCP,
在△OPQ中,QP=QO,
∴∠QOP=∠QPO,
又∵∠AOC=30°,
∴∠QPO=∠OCP+∠AOC=∠OCP+30°,
在△OPQ中,∠QOP+∠QPO+∠OQC=180°,
即(∠OCP+30°)+(∠OCP+30°)+∠OCP=180°,
整理得,3∠OCP=120°,
∴∠OCP=40°.
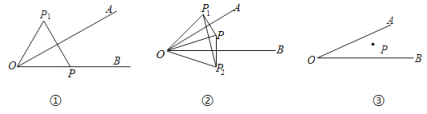
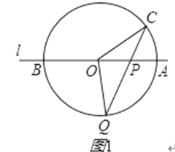
②当P在线段OA的延长线上(如图2)
∵OC=OQ,
∴∠OQP=(180°﹣∠QOC)×![]() ①,
①,
∵OQ=PQ,
∴∠OPQ=(180°﹣∠OQP)×![]() ②,
②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③得∠QOC=20°,则∠OQP=80°
∴∠OCP=100°;
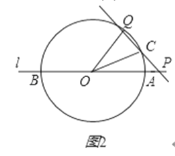
③当P在线段OA的反向延长线上(如图3),
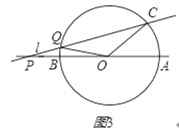
∵OC=OQ,
∴∠OCP=∠OQC=(180°﹣∠COQ)×![]() ①,
①,
∵OQ=PQ,
∴∠P=(180°﹣∠OQP)×![]() ②,
②,
∵∠AOC=30°,
∴∠COQ+∠POQ=150°③,
∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,
①②③④联立得
∠P=10°,
∴∠OCP=180°﹣150°﹣10°=20°.
故答案为:40°、20°、100°.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.