题目内容
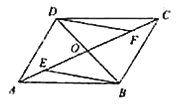
【题目】如图1,长方形OABC的边OA、OC分别在x轴、y轴上,B点坐标是(8,4),将△AOC沿对角线AC翻折得△ADC,AD与BC相交于点E.
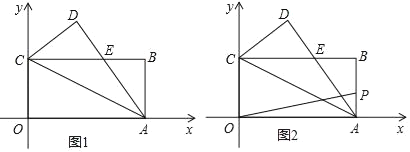
(1)求证:△CDE≌△ABE
(2)求E点坐标;
(3)如图2,动点P从点A出发,沿着折线A→B→C→O运动(到点O停止),是否存在点P,使得△POA的面积等于△ACE的面积,若存在,直接写出点P坐标,若不存在,说明理由.
【答案】(1)见解析;(2)E(5,4);(3)存在,满足条件的点P的坐标为(8,![]() )或(0,
)或(0,![]() ),理由见解析
),理由见解析
【解析】
(1)用角角边定理即可证明.
(2)设CE=AE=n,则BE=8-n,利用勾股定理即可求解.
(3)构建方程确定点P的纵坐标即可解决问题.
解:(1)证明:∵四边形OABC为矩形,
∴AB=OC,∠B=∠AOC=90°,
∴CD=OC=AB,∠D=∠AOC=∠B,
又∠CED=∠ABE,
∴△CDE≌△ABE(AAS),
∴CE=AE;
(2)∵B(8,4),即AB=4,BC=8.
∴设CE=AE=n,则BE=8﹣n,
可得(8﹣n)2+42=n2,
解得:n=5,
∴E(5,4);
(3)∵S△ACE=![]() CEAB=
CEAB=![]() ×5×4=10,
×5×4=10,
∴S△POA=![]() OAyP=10,
OAyP=10,
∴![]() ×8×yP=10,
×8×yP=10,
∴yP=![]() ,
,
∴满足条件的点P的坐标为(8,![]() )或(0,
)或(0,![]() ).
).

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】已知一水池的容积V(公升)与注入水的时间t(分钟)之间开始是一次函数关系,表中记录的是这段时间注入水的时间与水池容积部分对应值.
注入水的时间t(分钟) | 0 | 10 | … | 25 |
水池的容积V(公升) | 100 | 300 | … | 600 |
(1)求这段时间时V关于t的函数关系式(不需要写出函数的定义域);
(2)从t为25分钟开始,每分钟注入的水量发生变化了,到t为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.