题目内容
 如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为________.
如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为________.
8
分析:当抛物线y=a(x-m)2+n的顶点在线段AB的A点上时,点C的横坐标最小把A的坐标代入即可求出a的值,因为抛物线y=a(x-m)2+n的顶点在线段AB上运动,所以抛物线的a永远等于- ,根据题意可知当抛物线的顶点运动到B时,D的横坐标最大,把B的坐标和a的值代入即可求出二次函数的解析式,再求出y=0时x的值即可求出答案.
,根据题意可知当抛物线的顶点运动到B时,D的横坐标最大,把B的坐标和a的值代入即可求出二次函数的解析式,再求出y=0时x的值即可求出答案.
解答:当抛物线y=a(x-m)2+n的顶点在线段AB的A点上时,点C的横坐标最小,
把A(1,4)代入得:y=a(x-1)2+4,
把C(-3,0)代入得:0=a(-3-1)2+4,
解得:a=- ,
,
即:y=- (x-1)2+4,
(x-1)2+4,
∵抛物线y=a(x-m)2+n的顶点在线段AB上运动,
∴抛物线的a永远等于- ,
,
当抛物线的顶点运动到B时,D的横坐标最大,把a=- 和B(4,4)代入y=a(x-m)2+n得:
和B(4,4)代入y=a(x-m)2+n得:
y=- (x-4)2+4,
(x-4)2+4,
当y=0时,0=- (x-4)2+4,
(x-4)2+4,
解得:x1=0,x2=8,
∵C在D的左侧,
∴点D的横坐标最大值是8.
故答案为:8.
点评:本题主要考查了二次函数的性质,用待定系数法求二次函数的解析式,用直接开平方法解一元二次方程等知识点,理解题意并根据已知求二次函数的解析式是解此题的关键,此题是一个比较典型的题目.
分析:当抛物线y=a(x-m)2+n的顶点在线段AB的A点上时,点C的横坐标最小把A的坐标代入即可求出a的值,因为抛物线y=a(x-m)2+n的顶点在线段AB上运动,所以抛物线的a永远等于-
 ,根据题意可知当抛物线的顶点运动到B时,D的横坐标最大,把B的坐标和a的值代入即可求出二次函数的解析式,再求出y=0时x的值即可求出答案.
,根据题意可知当抛物线的顶点运动到B时,D的横坐标最大,把B的坐标和a的值代入即可求出二次函数的解析式,再求出y=0时x的值即可求出答案.解答:当抛物线y=a(x-m)2+n的顶点在线段AB的A点上时,点C的横坐标最小,
把A(1,4)代入得:y=a(x-1)2+4,
把C(-3,0)代入得:0=a(-3-1)2+4,
解得:a=-
 ,
,即:y=-
 (x-1)2+4,
(x-1)2+4,∵抛物线y=a(x-m)2+n的顶点在线段AB上运动,
∴抛物线的a永远等于-
 ,
,当抛物线的顶点运动到B时,D的横坐标最大,把a=-
 和B(4,4)代入y=a(x-m)2+n得:
和B(4,4)代入y=a(x-m)2+n得:y=-
 (x-4)2+4,
(x-4)2+4,当y=0时,0=-
 (x-4)2+4,
(x-4)2+4,解得:x1=0,x2=8,
∵C在D的左侧,
∴点D的横坐标最大值是8.
故答案为:8.
点评:本题主要考查了二次函数的性质,用待定系数法求二次函数的解析式,用直接开平方法解一元二次方程等知识点,理解题意并根据已知求二次函数的解析式是解此题的关键,此题是一个比较典型的题目.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
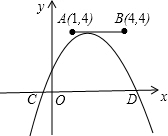 如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为
如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为 15、如图,点A、B的坐标分别为(1,2)、(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为
15、如图,点A、B的坐标分别为(1,2)、(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为
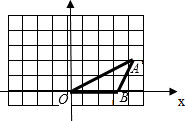 △OA′B′的位置
△OA′B′的位置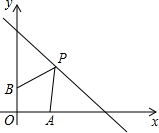 (2013•德惠市一模)如图,点A、B的坐标分别为(1,0)、(0,1),点P是第一象限内直线y=-x+3上的一个动点,当点P的横坐标逐渐增大时,四边形OAPB的面积( )
(2013•德惠市一模)如图,点A、B的坐标分别为(1,0)、(0,1),点P是第一象限内直线y=-x+3上的一个动点,当点P的横坐标逐渐增大时,四边形OAPB的面积( )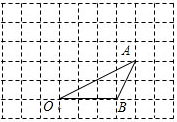 如图,点O、B的坐标分别为(0,0)(3,0),将△OAB绕O点按逆时针方向旋转90°得到△OA′B′.
如图,点O、B的坐标分别为(0,0)(3,0),将△OAB绕O点按逆时针方向旋转90°得到△OA′B′.