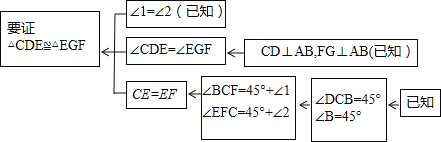
��Ŀ����
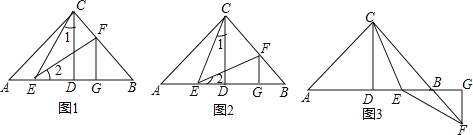
����Ŀ����ͼ���ڡ�ABC�У�AD�Ǹߣ�AE�ǽ�ƽ���ߣ���B=20�㣬��C=60�㣮
��1�����CAD����AEC�͡�EAD�Ķ�����
��2����ͼ�η����˱仯����֪�������Ƕ�����Ϊ������B=30�㣬��C=60�����EAD= �㣻
����B=50�㣬��C=60��ʱ�����EAD= �㣻
����B=60�㣬��C=60��ʱ�����EAD= �㣻
����B=70�㣬��C=60��ʱ�����EAD= �㣮
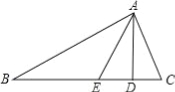
��3������B�͡�C�Ķ�����Ϊ����ĸ���ͦ�����ʾ�������ҵ���EAD����ͦ�֮��Ĺ�ϵ����ֱ��д���㷢�ֵĽ��ۣ�
���𰸡���1������CAD=30������AEC=70������EAD=20������2����15����5����0����5������3������������ʱ����EAD=���©�����������������ʱ����EAD=�������£���
��������
�����������1����������B����C�Ķ����ó���BAC�Ķ��������ݽ�ƽ���ߵ����ʵó���EAC�Ķ��������ݸ��ߵ����ʵó���CAD�Ķ�����������EAD=��EAC����DAC����AEC=180�㩁��EAC����C�ó��Ƕȣ���2����������EAD=��EAC����DAC������EAD=��DAC����EAC����Ƕȣ���3������������ʱ��������EAD=��EAC����DAC�ó��Ƕȣ���������ʱ��������EAD=��DAC����EAC�ó��Ƕ�.
�����������1�����ߡ�B=20�㣬��C=60�㣬
���BAC=180�㩁20�㩁60��=100�㣬��AE�ǽ�ƽ���ߣ����EAC=50�㣬
��AD�Ǹߣ����ADC=90�㣬���CAD=30�㣬
���EAD=��EAC����DAC=50�㩁30��=20�㣬
���AEC=180�㩁��EAC����C=180�㩁50�㩁60��=70�㣻
��2�����١�EAD=��EAC����DAC=45�㩁30��=15�㣻
�ڡ�EAD=��EAC����DAC=35�㩁30��=5�㣻
�ۡ�EAD=��EAC����DAC=30�㩁30��=0�㣻
�ܡ�EAD=��DAC����EAC=30�㩁25��=5�㣻
��3����������ʱ��
���EAD=��EAC����DAC=[��90��![]() ���㩁��90�㩁�¡㣩]=���©�������
���㩁��90�㩁�¡㣩]=���©�������
��������ʱ��
���EAD=��DAC����EAC=[��90�㩁�¡㣩����90��![]() ����]=�������£���
����]=�������£���

 �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�