题目内容
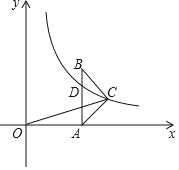
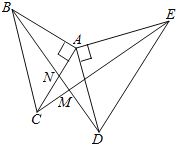
【题目】如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N.
(1)证明:BD=CE;
(2)证明:BD⊥CE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)要证明BD=CE,只要证明△ABD≌△ACE即可,两三角形中,已知的条件有AD=AE,AB=AC,那么只要再得出两对应边的夹角相等即可得出三角形全等的结论.我们发现∠BAD和∠EAC都是90°加上一个
∠CAD,因此∠CAE=∠BAD.由此构成了两三角形全等中的(SAS)因此两三角形全等.
(2)要证BD⊥CE,只要证明∠BMC是个直角就行了.由(1)得出的全等三角形我们可知:
∠ABN=∠ACE,三角形ABC中,∠ABN+∠CBN+∠BCN=90°,根据上面的相等角,我们可得出∠ACE+∠CBN+∠BCN=90°,即∠ABN+∠ACE=90°,因此∠BMC就是直角.
证明:(1)∵∠BAC=∠DAE=90°
∴∠BAC+∠CAD=∠DAE+∠CAD
即∠CAE=∠BAD
在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴BD=CE
(2)∵△ABD≌△ACE
∴∠ABN=∠ACE
∵∠ANB=∠CND
∴∠ABN+∠ANB=∠CND+∠NCE=90°
∴∠CMN=90°
即BD⊥CE.

练习册系列答案
相关题目