题目内容
【题目】如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15o,E为AD延长线上的一点,且CE=CA,若点M在DE上,且DC=DM。则下列结论:①∠ADB=120°;②△ADC≌△BDC;③线段DC所在的直线垂直平分AB;④ME=BD;正确的有( )
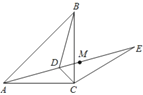
A. 1个B. 4个C. 2个D. 3个
【答案】B
【解析】
连接CM,求出∠DAB=∠DBA=30°,即可得∠ADB=120°;求出AD=BD,可证△ADC≌△BDC;求出∠ACD=∠BCD=45°,根据等腰三角形三线合一可得线段DC所在的直线垂直平分AB;求出∠MDC=60°,得等边三角形CMD,得出CM=CD,求出∠EMC=∠ADC=120°,证△ADC≌△EMC,推出AD=EM即可.
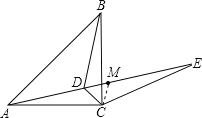
解:连接MC,在等腰直角△ABC中,
∵∠CAD=∠CBD=15°,
∴∠BAD=∠ABD=45°-15°=30°,
∴∠ADB=120°,故①正确;
∴BD=AD,
又∵AC=BC,∠CAD=∠CBD=15°,
∴△BDC≌△ADC(SSS),故②正确;
∴∠DCA=∠DCB=45°,即CD平分∠BCA,
∴线段DC所在的直线垂直平分AB,(等腰三角形三线合一),故③正确;
∴∠EDC=∠DAC+∠DCA=15°+45°=60°,
∵DC=DM,
∴△MDC是等边三角形,即CM=CD.
又∵∠EMC=180°-∠DMC=180°-60°=120°,
∠ADC=180°-∠MDC=180°-60°=120°,
∴∠EMC=∠ADC.
又∵CE=CA,
∴∠DAC=∠CEM=15°,
∴△ADC≌△EMC(AAS),
∴ME=AD=DB,
∴ME=BD,故④正确.
正确的有:①②③④.
故选B.

 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案【题目】已知:如图,四边形AOBC是矩形,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,3),∠OAB=60°,以AB为轴对折后,C点落在D点处,则D点的坐标为( )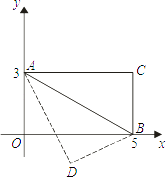
A.![]()
B.![]()
C.![]()
D.![]()
【题目】为了更好放松心情,上周六,小红妈妈开车带着小红一家到外郊游,出发前汽车油箱内有一定量的油.行驶过程中油箱中剩余油量![]() (升)与行驶时间
(升)与行驶时间![]() (小时)的关系如下表,请根据表格回答下列问题:
(小时)的关系如下表,请根据表格回答下列问题:
时间/小时 | 0 | 1 | 2 | 3 | 4 | 5 |
邮箱剩余油量/升 | 50 | 45 | 40 | 35 | 30 | 25 |
(1)汽车行驶前油箱里有_____________升汽油,汽车每小时耗油____________升;
(2)请写出![]() 与
与![]() 的关系式;
的关系式;
(3)当汽车行驶24小时时,油箱中还剩余多少升油?