��Ŀ����
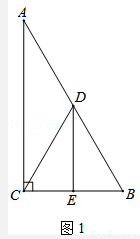
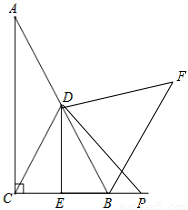
��Rt��ABC�У���ACB=90�㣬��A=30�㣬��D��AB���е㣬DE��BC������Ϊ��E������CD��
��1����ͼ1��DE��BC��������ϵ���� ����
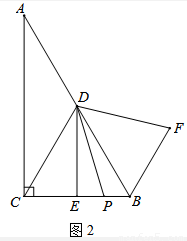
��2����ͼ2����P���߶�CB��һ���㣨��P�����B��C�غϣ�������DP�����߶�DP�Ƶ�D��ʱ����ת60�㣬�õ��߶�DF������BF�������DE��BF��BP����֮���������ϵ����֤����Ľ��ۣ�
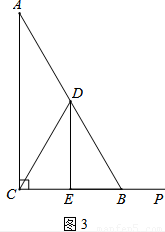
��3������P���߶�CB�ӳ�����һ���㣬���գ�2���е�����������ͼ3�в�ȫͼ�Σ���ֱ��д��DE��BF��BP����֮���������ϵ��
�⣺��1��DE= BC��
BC��
��2��������ת�����ʵõ���PDF=60�㣬DP=DF���á�CDP=��BDF�����ݡ�SAS�����жϡ�DCP�ա�DBF����CP=BF������CP=BC��BP��DE= BC�ɵõ�BF+BP=
BC�ɵõ�BF+BP=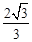 DE��
DE��
��3����ȫͼ����ͼ��DE��BF��BP����֮���������ϵΪBF��BP=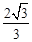 DE��
DE��
��������
�����������1���ߡ�ACB=90�㣬��A=30�㣬���B=60�㡣
�ߵ�D��AB���е㣬��DB=DC�����DCBΪ�ȱ������Ρ�
��DE��BC����DE= BC��
BC��
��2��������ת�����ʵõ���PDF=60�㣬DP=DF���á�CDP=��BDF�����ݡ�SAS�����жϡ�DCP�ա�DBF����CP=BF������CP=BC��BP��DE= BC�ɵõ�BF+BP=
BC�ɵõ�BF+BP=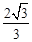 DE��
DE��
BF+BP=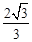 DE��֤�����£�
DE��֤�����£�
���߶�DP�Ƶ�D��ʱ����ת60�㣬�õ��߶�DF�����PDF=60�㣬DP=DF��
�ߡ�CDB=60�㣬���CDB����PDB=��PDF����PDB�������CDP=��BDF��
�ڡ�DCP�͡�DBF�У���DC=DB����CDP=��BDF��DP=DF��
���DCP�ա�DBF��SAS������CP=BF��
��CP=BC��BP����BF+BP=BC��
���ɣ�1��DE= BC����BC=
BC����BC=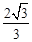 DE����BF+BP=
DE����BF+BP=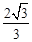 DE��
DE��
��3���루2��һ����֤����DCP�ա�DBF����CP=BF��
��CP=BC+BP����BF��BP=BC=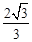 DE����
DE����
��ȫͼ����ͼ��DE��BF��BP����֮���������ϵΪBF��BP=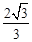 DE��
DE��


| A��asinA | ||
B��
| ||
| C��acosA | ||
D��
|
 ��ͼ����Rt��ABC�У���C=90�㣬CD��AB��D����AD��BD=9��4����AC��BC��ֵΪ��������
��ͼ����Rt��ABC�У���C=90�㣬CD��AB��D����AD��BD=9��4����AC��BC��ֵΪ��������| A��9��4 | B��9��2 | C��3��4 | D��3��2 |
 ��֪����ͼ����Rt��ABC�У���C=90�㣬AC=12��BC=9��D��AB��һ�㣬��BDΪֱ���ġ�O��AC��E�����O�İ뾶��
��֪����ͼ����Rt��ABC�У���C=90�㣬AC=12��BC=9��D��AB��һ�㣬��BDΪֱ���ġ�O��AC��E�����O�İ뾶�� ��ͼ����֪����Rt��ABC�У���C=90�㣬AB=12����D��AB���е㣬��O�ǡ�ABC�����ģ���OD�ij�Ϊ��������
��ͼ����֪����Rt��ABC�У���C=90�㣬AB=12����D��AB���е㣬��O�ǡ�ABC�����ģ���OD�ij�Ϊ��������