题目内容
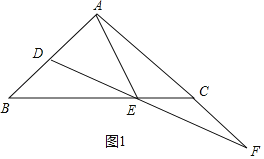
【题目】如图，△ABC中，AB=AC，∠BAC=90°，点D，E分别在AB，BC上，∠EAD=∠EDA，点F为DE的延长线与AC的延长线的交点．
（1）求证：DE=EF；
（2）判断BD和CF的数量关系，并说明理由；
（3）若AB=3，AE=
，求BD的长．
【答案】（1）证明见解析；（2证明见解析；（3）BD=1.
【解析】
（1）先根据等角对等边得出EA=ED，再在Rt△ADF中根据直角三角形的两锐角互余和等角的余角相等得出∠EAC=∠F，得出EA=EF，等量代换即可解决问题；
（2）结论：BD=CF．如图2中，在BE上取一点M，使得ME=CE，连接DM．想办法证明DM=CF，DM=BD即可；
（3）如图3中，过点E作EN⊥AD交AD于点N．设BD=x，则DN=
，DE=AE=
，由∠B=45°，EN⊥BN．推出EN=BN=x+=
，在Rt△DEN中，根据DN2+NE2=DE2，构建方程即可解决问题．
（1）证明：如图1中，
，
，
，
，
，
，
，
．
（2）解：结论：
．
理由：如图2中，在
上取一点
，使得
，连接
．
．
，
．
，
，
，
，
，
，
，
，
．
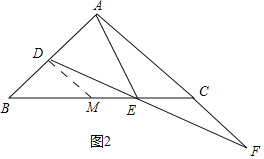
（3）如图3中，过点
作
交
于点
．
，，
，
设
，则
，
，
，
．
，
在
中，
，
解得
或
（舍弃）
．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
