题目内容
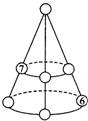 将1~7这五个自然数填入圆锥体中各圆圈内,使三条线段上三数之和、两圆周上三数之和都等于12.
将1~7这五个自然数填入圆锥体中各圆圈内,使三条线段上三数之和、两圆周上三数之和都等于12.
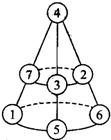 解:如图所示:
解:如图所示:∵1+2+3+4+5+6+7=28,12×2=24,
∴顶点处为28-24=4.
则左下方为12-4-7=1,4的下方为12-1-6=5,中间为12-4-5=3,右边的中间为12-4-6=2.
分析:两个圆周加上顶点处的数的和应为1+2+3+4+5+6+7=28,而两圆周上数的和为12×2=24,故顶点处应填28-24=4.则其余各点容易得出.
点评:此题通过圆锥体考查有理数加法,此题类似于填幻方,观察发现先填出顶点处的数是解决这类问题的关键.

练习册系列答案
相关题目
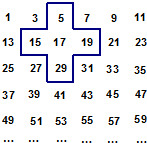 将连续的奇数1,3,5,7,…,排成如图所示的数表,用十字框任意框出5个数.
将连续的奇数1,3,5,7,…,排成如图所示的数表,用十字框任意框出5个数.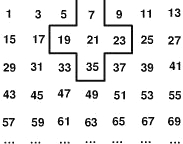
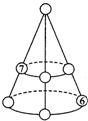 23、将1~7这五个自然数填入圆锥体中各圆圈内,使三条线段上三数之和、两圆周上三数之和都等于12.
23、将1~7这五个自然数填入圆锥体中各圆圈内,使三条线段上三数之和、两圆周上三数之和都等于12.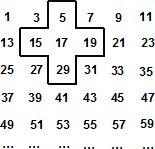 将连续的奇数1,3,5,7,…,排成如下图的数表,用图中所示的十字框可任意框出5个数.
将连续的奇数1,3,5,7,…,排成如下图的数表,用图中所示的十字框可任意框出5个数.