题目内容
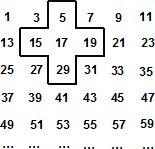 将连续的奇数1,3,5,7,…,排成如下图的数表,用图中所示的十字框可任意框出5个数.
将连续的奇数1,3,5,7,…,排成如下图的数表,用图中所示的十字框可任意框出5个数.【探究规律一】:设十字框中间的奇数为a,则框中五个奇数之和用含a的代数式表示为
5a
5a
.【结论】:这说明能被十字框框中的五个奇数之和一定是自然数p的奇数倍,这个自然数p是
5
5
.【探究规律二】:落在十字框中间且又是第二列的奇数是15,27,39,51…则这一列数可以用代数式表示为12m+3(m为正整数),同样,落在十字框中间且又是第三列,第四列的奇数分别可表示为
12m+5,13m+7
12m+5,13m+7
.【运用规律】:
(1)已知被十字框框中的五个奇数之和为6025,则十字框中间的奇数是
1025
1025
;这个奇数落在从左往右第3
3
列.(2)被十字框框中的五个奇数之和可能是485吗?可能是3045吗?说说你的理由.
分析:探究规律一:可设正中间的数为a,根据表中框的数得到其余数的表示方法,相加即可;看含有哪个因数即可;
探究规律二:若为第二列的奇数,起始数为3,每相邻2个数之间的数相隔12,那么这列的数是在3的基础上增加几个12;
同理可得其余列数中的奇数与各列起始数之间的关系即可;
运用规律:(1)6025÷5即可得到中间的数,根据中间的数÷12得到的余数,看符合第一行中的哪个奇数,即可得到相应的列数;
(2)除以5后看在哪一列,若在最左边一列或最右边一列则不能反之则能;
探究规律二:若为第二列的奇数,起始数为3,每相邻2个数之间的数相隔12,那么这列的数是在3的基础上增加几个12;
同理可得其余列数中的奇数与各列起始数之间的关系即可;
运用规律:(1)6025÷5即可得到中间的数,根据中间的数÷12得到的余数,看符合第一行中的哪个奇数,即可得到相应的列数;
(2)除以5后看在哪一列,若在最左边一列或最右边一列则不能反之则能;
解答:解:探究规律一:设正中间的数为a,易得上下,左右2数之和均为中间数的2倍,则5个数之和为2a+2a+a=5a;其中含有因数5,所以一定是5的倍数;
故答案为5a;5;
探究规律二:若为第三列的奇数,起始数为5,每相邻2个数之间的数相隔12,
∴这列的数为5+12m;
同理可得第四列的奇数分别可表示为 12m+7.
故答案为12m+5,12m+7.
(1)6025÷5=1025;1025÷12=502…5,所以在第3列,
(2)不可能是485,可能是3045,
(∵485÷5=97=12×8+1,即:中间的数在第一列,不可能;
3045÷5=609=12×50+9,即:中间的数在第五列,可能)
故答案为5a;5;
探究规律二:若为第三列的奇数,起始数为5,每相邻2个数之间的数相隔12,
∴这列的数为5+12m;
同理可得第四列的奇数分别可表示为 12m+7.
故答案为12m+5,12m+7.
(1)6025÷5=1025;1025÷12=502…5,所以在第3列,
(2)不可能是485,可能是3045,
(∵485÷5=97=12×8+1,即:中间的数在第一列,不可能;
3045÷5=609=12×50+9,即:中间的数在第五列,可能)
点评:考查对数字规律的得到及运用;发现相应规律是解决本题的关键.

练习册系列答案
相关题目
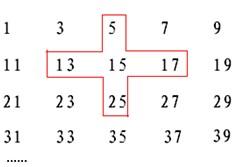
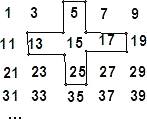 将连续的奇数1,3,5,7,9…,排成如图的数表,问:
将连续的奇数1,3,5,7,9…,排成如图的数表,问: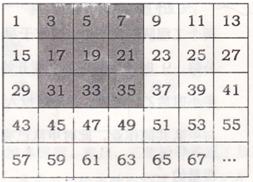
 将连续的奇数1,3,5,7,…排成如下数字表,用十子框框出5个数,如图所示.
将连续的奇数1,3,5,7,…排成如下数字表,用十子框框出5个数,如图所示.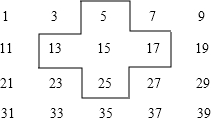 将连续的奇数1,3,5,7,9…排成如图的数表:
将连续的奇数1,3,5,7,9…排成如图的数表: