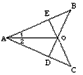
题目内容
已知：如图，在△ABC中，∠ABC=90°，F是AC上一点，且FB=FC，延长BC到点E，使BE=AC，过点E作ED⊥BF交BF的延长线于点D。求证：ED=AB。
证明：∵FB=FC，∴∠FBC=∠FCB。（1分）
∵ED⊥BF，∴∠EDB=90°。
∴∠ABC=∠EDB。（2分）
在△ABC和△EDB中，
∴△ABC
△EDB（AAS）。（4分）
∴ED=AB。（5分）
练习册系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
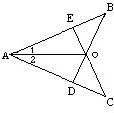34、已知：如图，在AB、AC上各取一点，E、D，使AE=AD，连接BD，CE，BD与CE交于O，连接AO，∠1=∠2，
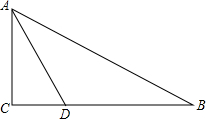（2013•启东市一模）已知，如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．
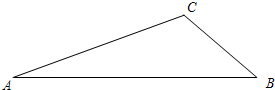已知：如图，在△ABC中，∠C=120°，边AC的垂直平分线DE与AC、AB分别交于点D和点E．
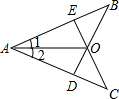已知：如图，在AB、AC上各取一点E、D，使AE=AD，连接BD，CE，BD与CE交于O，连接AO，∠1=∠2，