Question

【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.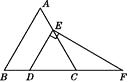

（1）求∠F的度数;
（2）若CD=2,求DF的长.

Answer 1

【答案】
（1）解：∵△ABC是等边三角形,
∴∠B=60°.
∵DE∥AB,
∴∠EDC=∠B=60°.
∵EF⊥DE,
∴∠DEF=90°.
∴∠F=90°-∠EDC=30° 。
（2）解：∵∠ACB=60°,∠EDC=60°,
∴∠DEC=60°.
∴△EDC是等边三角形.
∴DE=DC=2.
∵∠DEF=90°,∠F=30°,
∴DF=2DE=4 。
【解析】(1)根据等边三角形的性质得出∠B=60°，根据二直线平行同位角相等得出∠EDC=∠B=60°，根据垂直的定义得出∠DEF=90°，从而根据直角三角形的两锐角互余得出∠F=90°-∠EDC=30° ；
（2）根据三角形的内角和得出∠DEC=60°，根据三内角相等的三角形是等边三角形得出△EDC是等边三角形，根据等边三角形三边相等得出DE=DC=2，根据含30°的直角三角形的边之间的关系得出DF=2DE=4 。