��Ŀ����
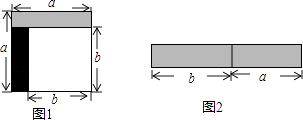
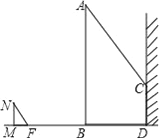
����Ŀ������˼����С����̽������ֱ�ߵ�λ�ù�ϵ��������ʱ�������ˡ��д������Ρ��������������ഹֱ�������γ�Ϊ���д������Ρ�����ͼ��1����ͼ��2����ͼ��3���У�AM��BN�ǡ�ABC�����ߣ�AM��BN�ڵ�P�����ABC�����������ξ�Ϊ���д������Ρ�����BC=a��AC=b��AB=c��
������̽����
��1����ͼ1����tan��PAB=1��c=4![]() ʱ��a=������b=������
ʱ��a=������b=������
��ͼ2������PAB=30�㣬c=2ʱ��a=������b=������
������֤����
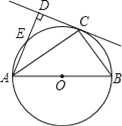
��2������۲죨1���еļ�����������a2��b2��c2����֮��Ĺ�ϵ���õ�ʽ��ʾ������������ͼ3֤����Ľ��ۣ�
����չ֤����
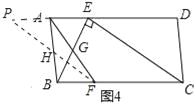
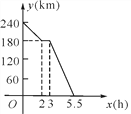
��3����ͼ4��ABCD�У�E��F�ֱ���AD��BC�����ȷֵ㣬��AD=3AE��BC=3BF������AF��BE��CE����BE��CE��E��AF��BE�ཻ��G��AD=3![]() ��AB=3����AF�ij���
��AB=3����AF�ij���

���𰸡���1��4![]() ��4
��4![]() ��
��![]() ��
��![]() ����2��a2+b2=5c2�����ɼ�����.(3)4.
����2��a2+b2=5c2�����ɼ�����.(3)4.
�������������������1��������֤����APB����PEF���ǵ���ֱ�������Σ����PA��PB��PE��PF�������ù��ɶ������ɽ�����⣮������EF����RT��PAB��RT��PEF�У�����30���������PA��PB��PE��PF�������ù��ɶ������ɽ�����⣮��2������a2+b2=5c2����MP=x��NP=y����AP=2x��BP=2y�����ù��ɶ����ֱ����a2��b2��c2���ɽ�����⣮��3��ȡAB�е�H������FH�����ӳ���DA���ӳ�����P�㣬����֤����ABF���д������Σ����ã�2���н����г����̼��ɽ�����⣮
�����������1���⣺��ͼ1�У���CE=AE��CF=BF��
��EF��AB��EF=![]() AB=2
AB=2![]() ��
��
��tan��PAB=1��
���PAB=��PBA=��PEF=��PFE=45����
��PF=PE=2��PB=PA=4��
��AE=BF=![]() =2
=2![]() ��
��
��b=AC=2AE=4![]() ��a=BC=4
��a=BC=4![]() ��
��
��ͼ2�У�����EF��
����CE=AE��CF=BF��
��EF��AB��EF=![]() AB=1��
AB=1��
�ߡ�PAB=30����
��PB=1��PA=![]() ��
��
��RT��EFP�У��ߡ�EFP=��PAB=30����
��PE=![]() ��PF=
��PF=![]() ��
��
��AE=![]() =
=![]() ��BF=
��BF=![]() =
=![]() ��
��
��a=BC=2BF=![]() ��b=AC=2AE=
��b=AC=2AE=![]() ��
��
��2������
֤������ͼ3�У�����EF��
��AF��BE�����ߣ�
��EF��AB��EF=![]() AB��
AB��
���FPE�ס�APB��
��![]() =
=![]() =
=![]() ��
��
��FP=x��EP=y����AP=2x��BP=2y��
��a2=BC2=4BF2=4��FP2+BP2��=4x2+16y2��
b2=AC2=4AE2=4��PE2+AP2��=4y2+16x2��
c2=AB2=AP2+BP2=4x2+4y2��
��a2+b2=20x2+20y2=5��4x2+4y2��=5c2��
��3���⣺��ͼ4�У�����AGE����FGB�У�
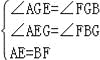 ��
��
���AGE�ա�FGB��
��BG=FG��ȡAB�е�H������FH�����ӳ���DA���ӳ�����P�㣬
ͬ����֤��APH�ա�BFH��
��AP=BF��PE=CF=2BF��
��PE��CF��PE=CF��
���ı���CEPF��ƽ���ı��Σ�
��FP��CE��
��BE��CE��
��FP��BE����FH��BG��
���ABF���д������Σ�
�ɣ�2����֪AB2+AF2=5BF2��
��AB=3��BF=![]() AD=
AD=![]() ��
��
��9+AF2=5����![]() ��2��
��2��
��AF=4��