��Ŀ����
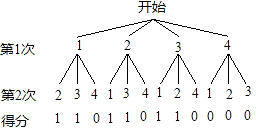
����Ŀ��Ϊ�˾���˭����ý��е�һ�ſ��ձ����볡ȯ��������������µ�һ����Ϸ�� �ڴ����б�ŷֱ�Ϊ1��2��3�ĺ��������ͱ��Ϊ4�İ���һ�����ĸ��������ɫ���Ų�ͬ�⣬û���κα����������֮ǰ��С����ȣ�������˶������۾����ȼ������Σ�ÿ������һ���Ѽ�������������Żؿڴ�������������ֻ��һ����������������������Ǻ�ɫ����1�֣�����0�֣���������������ǰ�ɫ���ҵ�1�֣������ҵ�0�֣��÷ָߵĻ���볡ȯ������÷���ͬ����Ϸ������
��1�������б�����״ͼ���1�ֵĸ��ʣ�
��2�������Ϸ�Ƿ�ƽ����˵�����ɣ�
���𰸡�
��1���⣺�б��ã�
1 | 2 | 3 | 4 | |
1 | �� | 1�� | 1�� | 0�� |
2 | 1�� | �� | 1�� | 0�� |
3 | 1�� | 1�� | �� | 0�� |
4 | 0�� | 0�� | 0�� | �� |
����״ͼͼ�ã�
��P����1�֣�= ![]()
��2���⣺����ƽ��
��P���ҵ�1�֣�= ![]()
��P����1�֣���P���ҵ�1�֣���
���ƽ
����������1�����ȸ��������г��������״ͼͼ��Ȼ��������еȿ��ܵĽ�����1�ֵ������Ȼ�����ø��ʹ�ʽ��⼴����ô𰸣���2���ɣ�1������ҵĵ÷֣��Ƚϸ��ʲ���ȣ����ɵ������Ϸ�Dz���ƽ��

��ϰ��ϵ�д�
 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
�����Ŀ