题目内容
【题目】在矩形![]() 中,点
中,点![]() 、
、![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 、
、![]() 、
、![]() 的中点,顺次连接
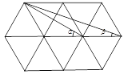
的中点,顺次连接![]() 所得的四边形我们称之为中点四边形,如图.
所得的四边形我们称之为中点四边形,如图.
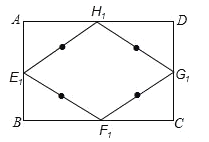
(1)求证:四边形![]() 是菱形;
是菱形;
(2)设![]() 的中点四边形是
的中点四边形是![]() ,
,![]() 的中点四边形是
的中点四边形是![]() ….
….![]() 的中点四边形是
的中点四边形是![]() ,那么这些中点四边形形状的变化有没有规律性? (填“有”或“无”)若有,说出其中的规律性 ;
,那么这些中点四边形形状的变化有没有规律性? (填“有”或“无”)若有,说出其中的规律性 ;
(3)进一步:如果我们规定:矩形![]() ,菱形
,菱形![]() ,并将矩形
,并将矩形![]() 的中点四边形用
的中点四边形用![]() 表示;菱形的中点四边形用
表示;菱形的中点四边形用![]() 表示,由题(1)知,
表示,由题(1)知,![]() ,那么
,那么![]() .
.
【答案】(1)见解析;(2)有;矩形的中点四边形是菱形,菱形的中点四边形是矩形;(3)菱形的中点四边形为矩形可以表示为:![]() .
.
【解析】
(1)因为题中给出的条件是中点,所以可利用三角形中位线性质,以及矩形对角线相等去证明四条边都相等,从而说明是一个菱形.
(2)仔细观察,发现这两个四边形互为中点四边形.
(3)根据上题总结的规律可以得到菱形的中点四边形为矩形.
(1)证明:连接![]() 、
、![]() ,
,
![]() 点
点![]() 、
、![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 、
、![]() 、
、![]() 的中点,
的中点,
![]()
![]() ,同理
,同理![]() ,
,![]() ,
,![]() ,
,
又![]() 在矩形
在矩形![]() 中,
中,![]() ,
,
![]()
![]() ,
,
![]() 四边形
四边形![]() 是菱形.
是菱形.
(2)解:有;矩形的中点四边形是菱形,菱形的中点四边形是矩形.
(3)解:![]() 矩形的中点四边形为菱形,
矩形的中点四边形为菱形,
即:![]() ,
,
![]() 菱形的中点四边形为矩形可以表示为:
菱形的中点四边形为矩形可以表示为:![]() .
.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目