题目内容
已知抛物线y=ax2+6ax+c交x轴负半轴于A,B两点,以AB为边的矩形ABCD的顶点C,D在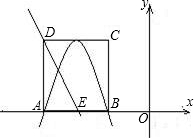 第二象限,过D点的直线y=ax+3a与x轴交于E.
第二象限,过D点的直线y=ax+3a与x轴交于E.(1)求S△ADE:S矩形ABCD;
(2)当S△ADE=1,且抛物线的顶点在CD边上时,求抛物线的解析式;
(3)在(2)中抛物线上是否存在一点P,使△APB为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(1)根据抛物线的解析式可得,抛物线的对称轴为x=-3,由直线DE的解析式可得E(-3,0),因此点E正好在抛物线的对称轴上,即AE=
AB,然后分别表示出△ADE和矩形的面积,即可得到它们的比例关系.
(2)利用抛物线的解析式,可求得抛物线的顶点坐标,和A、B两点的坐标,即可得到AB、AD的长,然后分别表示出△ADE和矩形的面积表达式,联立两式即可求得a、c的值.
(3)根据抛物线的解析式可得到A、B的坐标,显然A、B都不可能是直角顶点,那么只有一种可能,即∠APB=90°,可设出点P的坐标,利用AP⊥BP,即两直线的斜率的积为-1即可求得点P的坐标.
| 1 |
| 2 |
(2)利用抛物线的解析式,可求得抛物线的顶点坐标,和A、B两点的坐标,即可得到AB、AD的长,然后分别表示出△ADE和矩形的面积表达式,联立两式即可求得a、c的值.
(3)根据抛物线的解析式可得到A、B的坐标,显然A、B都不可能是直角顶点,那么只有一种可能,即∠APB=90°,可设出点P的坐标,利用AP⊥BP,即两直线的斜率的积为-1即可求得点P的坐标.
解答:解:(1)易知:抛物线的对称轴为x=-3,E(-3,0);
则E点在抛物线的对称轴上,
即AE=BE=
AB;
由于S△ADE=
AE•AD=
AB•AD=
S矩形ABCD;
故S△ADE:S矩形ABCD=1:4.
(2)由(1)知:S矩形ABCD=4S△ADE=4;
∴AB═BC=2,
∵E(-3,0),
∴抛物线的顶点坐标为:(-3,2),B(-2,0),
设y=a(x+3)2+2,
∴a+2=0,
解得:a=-2,
∴抛物线的解析式为:y=-2(x+3)2+2=-2x2-12x-16.

(3)根据(2)得A(-4,0),B(-2,0);
设P(x,-2x2-12x-16),
由于∠PAB和∠PBA都不可能是直角,
则只有一种情况:AP⊥PB,
∵互相垂直的两条直线的斜率的积等于-1,
∴
•
=-1,
整理得:4x2+24x+33=0,
解得x=
,
代入抛物线的解析式中,可得P点坐标为:
P(
,
)或(
,
).
则E点在抛物线的对称轴上,
即AE=BE=
| 1 |
| 2 |
由于S△ADE=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
故S△ADE:S矩形ABCD=1:4.
(2)由(1)知:S矩形ABCD=4S△ADE=4;
∴AB═BC=2,
∵E(-3,0),
∴抛物线的顶点坐标为:(-3,2),B(-2,0),
设y=a(x+3)2+2,
∴a+2=0,
解得:a=-2,
∴抛物线的解析式为:y=-2(x+3)2+2=-2x2-12x-16.

(3)根据(2)得A(-4,0),B(-2,0);
设P(x,-2x2-12x-16),
由于∠PAB和∠PBA都不可能是直角,
则只有一种情况:AP⊥PB,
∵互相垂直的两条直线的斜率的积等于-1,
∴
| -2x2-12x-16 |
| x+4 |
| -2x2-12x-16 |
| x+2 |
整理得:4x2+24x+33=0,
解得x=
-6±
| ||
| 2 |
代入抛物线的解析式中,可得P点坐标为:
P(
-6+
| ||
| 2 |
| 1 |
| 2 |
-6-
| ||
| 2 |
| 1 |
| 2 |
点评:此题主要考查了矩形的性质、抛物线的对称性、图形面积的计算方法、二次函数解析式的确定以及直角三角形的判定方法等知识,由于此题的数据大都是未知数,而且计算量较大,因此难度也较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
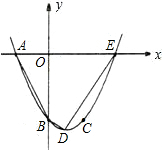 与x轴的另一个交点为E.
与x轴的另一个交点为E.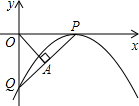 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=