题目内容
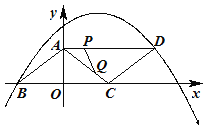
【题目】如图,□ABCD的两个顶点B,D都在抛物线y=![]() x2+bx+c上,且OB=OC,AB=5,tan∠ACB=
x2+bx+c上,且OB=OC,AB=5,tan∠ACB=![]() .
.
(1)求抛物线的解析式;
(2)在抛物线上是否存在点E,使以A,C,D,E为顶点的四边形是菱形?若存在,请求出点E的坐标;若不存在,请说明理由.
(3)动点P从点A出发向点D运动,同时动点Q从点C出发向点A运动,运动速度都是每秒1个单位长度,当一个点到达终点时另一个点也停止运动,运动时间为t(秒).当t为何值时,△APQ是直角三角形?
【答案】(1)y=![]() x2+
x2+![]() x+5;(2)存在点E的坐标为(4,6)(3)
x+5;(2)存在点E的坐标为(4,6)(3)![]() 或
或![]() .
.
【解析】试题分析:(1)根据平行四边形的性质,求出A、B、C、D坐标,然后用待定系数法求出函数的解析式;
(2)根据平行四边形的性质和菱形的判定,求出E点的坐标,然后判断其是否在函数的图像上即可;
(3)当△APQ是直角三角形时,分为∠APQ=90°或∠AQP=90°两种情况,通过解直角三角形求解即可.
试题解析:解:(1) ∵OB=OC,OA⊥BC,AB=5,∴AB= AC=5.
∴tan∠ACB=![]() =
=![]() ,∴
,∴![]() .
.
由勾股定理,得OA2+OC2=AC2, ∴(![]() )2+OC2=52,解得OC=±4(负值舍去) .
)2+OC2=52,解得OC=±4(负值舍去) .
∴![]() ,OB=OC=4,AD=BC=8.
,OB=OC=4,AD=BC=8.
∴A(0,3),B(-4,0) ,C(4,0) ,D(8,3) .
∴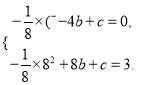
解之得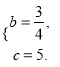
∴抛物线的解析式为y=![]() x2+
x2+![]() x+5.
x+5.
(2)存在.
∵四边形ABCD为平行四边形,∴AC=AB= CD.
又∵AD≠CD,
∴当以A,C,D,E为顶点的四边形是菱形时,AC=CD=DE=AE
由对称性可得,此时点E的坐标为(4,6)
当x=4时,y=![]() x2+
x2+![]() x+5=6,所以点(4,6)在抛物线y=
x+5=6,所以点(4,6)在抛物线y=![]() x2+
x2+![]() x+5上.
x+5上.
∴存在点E的坐标为(4,6)
(3) ∵四边形ABCD为平行四边形,∴AD∥BC,∴∠DAC=∠ACB<90°.
∴当△APQ是直角三角形时,∠APQ=90°或∠AQP=90°.
∵![]() ,∴
,∴![]() .
.
由题意可知AP=t,AQ=5-t,0≤t≤5.
当∠APQ=90°时, ![]() ,∴
,∴![]() ,解得
,解得![]() .
.
当∠AQP=90°时, ![]() ,∴
,∴![]() ,解得
,解得![]() .
.
∵![]() ,
, ![]()
∴![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案