ЬтФПФкШн
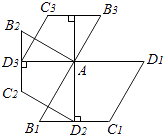
ЁОЬтФПЁПвбжЊAЁЂBдкЪ§жсЩЯЗжБ№БэЪОaЃЌbЃЎ
(1)ЖдееЪ§жсЬюаДЯТБэЃК
a | 6 | Ѓ6 | Ѓ6 | Ѓ6 | 2 | Ѓ1.5 |
b | 4 | 0 | 4 | Ѓ4 | Ѓ10 | Ѓ1.5 |
AЁЂBСНЕуЕФОрРы |
(2)ШєAЁЂBСНЕуМфЕФОрРыМЧЮЊdЃЌЪдЮЪЃКdКЭaЃЌbгаКЮЪ§СПЙиЯЕ?
(3)дкЪ§жсЩЯевГіЫљгаЗћКЯЬѕМўЕФећЪ§ЕуPЃЌЪЙЫќЕН5КЭЃ5ЕФОрРыжЎКЭЮЊ10ЃЌВЂЧѓЫљгаетаЉећЪ§ЕФКЭЃЛ
(4)ШєЕуCБэЪОЕФЪ§ЮЊxЃЌЕБЕуCдкЪВУДЮЛжУЪБЃЌ![]() ШЁЕУЕФжЕзюаЁ? зюаЁжЕЪЧЖрЩйЃП
ШЁЕУЕФжЕзюаЁ? зюаЁжЕЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉ2ЃЌ6ЃЌ10ЃЌ2ЃЌ12ЃЌ0ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ0ЃЛЃЈ4ЃЉЕуCдк-1КЭ2жЎМфЪБЃЌШЁЕУзюаЁжЕЮЊ3
ЃЛЃЈ3ЃЉ0ЃЛЃЈ4ЃЉЕуCдк-1КЭ2жЎМфЪБЃЌШЁЕУзюаЁжЕЮЊ3
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЪ§жсЩЯЕФСНЕуЃЌЧѓСНЕуОрРыМДПЩЃЛ
ЃЈ2ЃЉЪ§жсЩЯСНЕуМфЕФОрРыМДЮЊВюЕФОјЖджЕЃЛ
ЃЈ3ЃЉЕНСНЖЈЕуОрРыжЎКЭЕШгкСНЖЈЕужЎМфЕФОрРыЕФЕуЕФМЏКЯЪЧСНЖЈЕужЎМфЕФСЌЯпЃЌМДПЩЕУНтЃЛ
ЃЈ4ЃЉ![]() БэЪОxЕН-1ЕФОрРыЃЌЭЌРэ
БэЪОxЕН-1ЕФОрРыЃЌЭЌРэ![]() БэЪОxЕН2ЕФОрРыЃЌИУЬтМАзЊЛЏЮЊЪ§жсЩЯвЛЕуЕН-1КЭ2ЕФОрРыКЭзюаЁ.
БэЪОxЕН2ЕФОрРыЃЌИУЬтМАзЊЛЏЮЊЪ§жсЩЯвЛЕуЕН-1КЭ2ЕФОрРыКЭзюаЁ.
ЃЈ1ЃЉгЩЬтвтЃЌЕУ
AЁЂBСНЕуМфЕФОрРывРДЮЮЊЃК2ЃЌ6ЃЌ10ЃЌ2ЃЌ12ЃЌ0ЃЛ
ЃЈ2ЃЉгЩЬтвтЃЌЕУ
![]()
ЃЈ3ЃЉЕНСНЖЈЕуОрРыжЎКЭЕШгкСНЖЈЕужЎМфЕФОрРыЕФЕуЕФМЏКЯЪЧСНЖЈЕужЎМфЕФСЌЯп
ЙЪpЕувЛЖЈдк5КЭ-5жЎМф
етбљЕФећЪ§Еуга1,2,3,4,5,-5,-4,-3,-2,-1,0
ЙЪЫќУЧЕФКЭЮЊ0ЃЛ
ЃЈ4ЃЉгЩЬтвтЃЌЕУ
![]() БэЪОxЕН-1ЕФОрРыЃЌЭЌРэ
БэЪОxЕН-1ЕФОрРыЃЌЭЌРэ![]() БэЪОxЕН2ЕФОрРыЃЌ
БэЪОxЕН2ЕФОрРыЃЌ
ЁрЕуCдк-1КЭ2жЎМфЪБЃЌШЁЕУзюаЁжЕЃЌзюаЁжЕЮЊ3.