题目内容
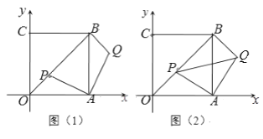
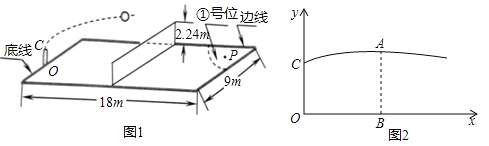
【题目】如图1,排球场长为18m,宽为9m,网高为2.24m.队员站在底线O点处发球,球从点O的正上方1.9m的C点发出,运动路线是抛物线的一部分,当球运动到最高点A时,高度为2.88m.即BA=2.88m.这时水平距离OB=7m,以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2.
(1)若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x取值范围).并判断这次发球能否过网?是否出界?说明理由;
(2)若球过网后的落点是对方场地①号位内的点P(如图1,点P距底线1m,边线0.5m),问发球点O在底线上的哪个位置?(参考数据:![]() 取1.4)
取1.4)
【答案】(1)这次发球过网,但是出界了,理由详见解析;(2)发球点O在底线上且距右边线0.1米处.
【解析】
(1)求出抛物线表达式,再确定x=9和x=18时,对应函数的值即可求解;
(2)当y=0时,y=﹣![]() (x﹣7)2+2.88=0,解得:x=19或﹣5(舍去﹣5),求出PQ=6
(x﹣7)2+2.88=0,解得:x=19或﹣5(舍去﹣5),求出PQ=6![]() =8.4,即可求解.
=8.4,即可求解.
(1)设抛物线的表达式为:y=a(x﹣7)2+2.88,
将x=0,y=1.9代入上式并解得:a=﹣![]() ,
,
故抛物线的表达式为:y=﹣![]() (x﹣7)2+2.88;
(x﹣7)2+2.88;
当x=9时,y=﹣![]() (x﹣7)2+2.88=2.8>2.24,
(x﹣7)2+2.88=2.8>2.24,
当x=18时,y=﹣![]() (x﹣7)2+2.88=0.64>0,
(x﹣7)2+2.88=0.64>0,
故这次发球过网,但是出界了;
(2)如图,分别过点作底线、边线的平行线PQ、OQ交于点Q,
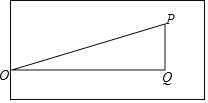
在Rt△OPQ中,OQ=18﹣1=17,
当y=0时,y=﹣![]() (x﹣7)2+2.88=0,解得:x=19或﹣5(舍去﹣5),
(x﹣7)2+2.88=0,解得:x=19或﹣5(舍去﹣5),
∴OP=19,而OQ=17,
故PQ=6![]() =8.4,
=8.4,
∵9﹣8.4﹣0.5=0.1,
∴发球点O在底线上且距右边线0.1米处.

【题目】为了了解同学们寒假期间每天健身的时间![]() (分),校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表,已知
(分),校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表,已知![]() 组所在扇形的圆心角为
组所在扇形的圆心角为![]() .
.
组别 | 频数统计 |
| 8 |
| 12 |
|
|
| 15 |
| b |
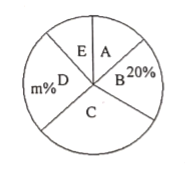
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有 人,![]() ,
,![]() ,
,![]() ;
;
(2)求扇形统计图中扇形![]() 的圆心角度数;
的圆心角度数;
(3)该校共有学生1200人,请估计每天健身时间不少于1小时的人数.
【题目】某公司其有![]() 名销售人员,为了解该公司销售人员某季度商品销售情况,随机抽取部分销售人员该季度的销售数量,并把所得数据整理后绘制成如下统计图表进行分析.
名销售人员,为了解该公司销售人员某季度商品销售情况,随机抽取部分销售人员该季度的销售数量,并把所得数据整理后绘制成如下统计图表进行分析.
频率分布表
组别 | 销售数量(件) | 频数 | 频率 |
A |
|
|
|
B |
|
|
|
C |
|
|
|
D |
|
|
|
E |
|
|
|
合计 |
|
| |
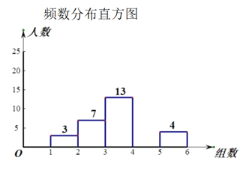
请根据以上信息,解决下列问题:
(1)频数分布表中,![]() ________、
________、![]() ________:
________:
(2)补全频数分布直方图;
(3)如果该季度销量不低于![]() 件的销售人员将被评为“优秀员工”,试估计该季度被评为“优秀员工”的人数.
件的销售人员将被评为“优秀员工”,试估计该季度被评为“优秀员工”的人数.