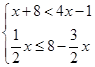题目内容
已知 的半径
的半径 =2,
=2, 的半径
的半径 是方程
是方程 的根,
的根, 与
与 的圆心距为1,那么两圆的位置关系为
的圆心距为1,那么两圆的位置关系为
 的半径
的半径 =2,
=2, 的半径
的半径 是方程
是方程 的根,
的根, 与
与 的圆心距为1,那么两圆的位置关系为
的圆心距为1,那么两圆的位置关系为| A.内含 | B.内切 | C.相交 | D.外切 |
B。
解 得,x=3,经检验x=3是原方程的根,所以
得,x=3,经检验x=3是原方程的根,所以 。
。
根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。因此,
∵⊙O1和⊙O2的半径分别为 =2和
=2和 ,且O1O2=1,
,且O1O2=1,
∴3-2=1,即两圆圆心距离等于两圆半径之差。
∴⊙O1和⊙O2的位置关系是内切。故选B。
 得,x=3,经检验x=3是原方程的根,所以
得,x=3,经检验x=3是原方程的根,所以 。
。根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。因此,
∵⊙O1和⊙O2的半径分别为
 =2和
=2和 ,且O1O2=1,
,且O1O2=1,∴3-2=1,即两圆圆心距离等于两圆半径之差。
∴⊙O1和⊙O2的位置关系是内切。故选B。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
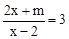 的解是正数,则m的取值范围是 。
的解是正数,则m的取值范围是 。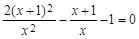
 ,现由徒弟先做1天,师徒再合作2天完成。
,现由徒弟先做1天,师徒再合作2天完成。 ,然后从-1、1、2三个数中选取一个你认为合适的数作为x的值代入求值.
,然后从-1、1、2三个数中选取一个你认为合适的数作为x的值代入求值.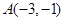 在反比例函数
在反比例函数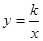 的图像上,则分式方程
的图像上,则分式方程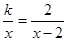 的解是
的解是



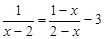 ;(2)解不等式组:
;(2)解不等式组: