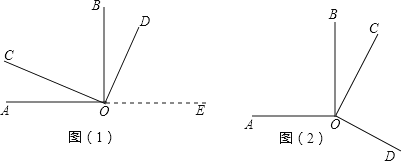题目内容
【题目】在正方形ABCD中,BD是一条对角线,点P在射线CD上(与点C、D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于H,连接AH,PH.
(1)若点P在线段CD上,如图1.
①依题意补全图1;
②判断AH与PH的数量关系与位置关系并加以证明;
(2)若点P在线段CD的延长线上,且∠AHQ=152°,正方形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)
【答案】
(1)
解:①如图1;

②解法一:如图1,连接CH,
∵四边形ABCD是正方形,QH⊥BD,
∴∠HDQ=45°,
∴△DHQ是等腰直角三角形.
∵DP=CQ,
在△HDP与△HQC中.
 ,
,
∴△HDP≌△HQC(SAS),
∴PH=CH,∠HPC=∠HCP.
∵BD是正方形ABCD的对称轴,
∴AH=CH,∠DAH=∠HCP,
∴∠AHP=180°﹣∠ADP=90°,
∴AH=PH,AH⊥PH.
解法二:如图1,连接CH,
∵QH⊥BD,
∴∠QHB=∠BCQ=90°,
∴B、H、C、Q四点共圆,
∴∠DHC=∠BQC,
由正方形的性质可知∠DHC=∠AHD,
由平移性质可知∠BQC=∠APD,
∴∠AHD=∠APD,
∴A、H、P、D四点共圆,
∴∠PAH=∠PDH=45°,∠AHP=∠ADP=90°,
∴△HAP是等腰直角三角形,
∴AH=PH,AH⊥PH.
(2)
解法一:如图2,

∵四边形ABCD是正方形,QH⊥BD,
∴∠HDQ=45°,
∴△DHQ是等腰直角三角形.
∵△BCQ由△ADP平移而成,
∴PD=CQ.
作HR⊥PC于点R,
∵∠AHQ=152°,
∴∠AHB=62°,
∴∠DAH=17°.
设DP=x,则DR=HR=RQ=![]()
∵tan17°=![]() ,即tan17°=
,即tan17°=![]() ,
,
∴x=![]() .
.
解法二:
由(1)②可知∠AHP=90°,
∴∠AHP=∠ADP=90°,
∴A、H、D、P四点共圆,
又∠AHQ=152°,∠BHQ=90°,
∴∠AHB=152°﹣90°=62°,
由圆的性质可知∠APD=∠AHB=62°,
在Rt△APD中,∠PAD=90°﹣62°=28°,
∴PD=ADtan28°=tan28°.
【解析】(1)①根据题意画出图形即可;
②连接CH,先根据正方形的性质得出△DHQ是等腰直角三角形,再由SAS定理得出△HDP≌△HQC,故PH=CH,∠HPC=∠HCP,由正方形的性质即可得出结论;
(2)根据四边形ABCD是正方形,QH⊥BD可知△DHQ是等腰直角三角形,再由平移的性质得出PD=CQ.作HR⊥PC于点R,由∠AHQ=152°,可得出∠AHB及∠DAH的度数,设DP=x,则DR=HR=RQ,由锐角三角函数的定义即可得出结论.
【考点精析】利用平行四边形的判定与性质对题目进行判断即可得到答案,需要熟知若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.

 名校课堂系列答案
名校课堂系列答案【题目】LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点,在日常生活中,人们更倾向于LED灯的使用,某校数学兴趣小组为了解LED灯泡与普通白炽灯泡的销售情况,进行了市场调查:某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |

(1)该商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡按标价进行销售,而普通白炽灯泡打九折销售,当销售完这批灯泡后可以获利3200元,求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的30%,并求出此时这批灯泡的总利润为多少元?