Question

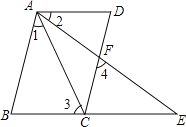
【题目】如图，在平行四边形ABCD中，点O是边BC的中点，连接AO并延长，交DC延长线于点E，连接AC，BE．

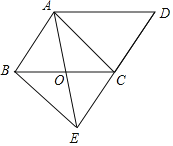
（1）求证：四边形ABEC是平行四边形；

（2）当∠D＝50°，∠AOC＝100°时，判断四边形ABEC的形状，并说明理由．

Answer 1

【答案】（1）见解析；（2）四边形ABEC是矩形，理由见解析.

【解析】

（1）由平行四边形的性质可得AB∥CD，可得∠BAO＝∠CEO，∠ABO＝∠ECO，由“AAS”可证△ABO≌△ECO，可得AO＝EO，即可证四边形ABEC是平行四边形；

（2）由平行四边形的性质和三角形外角性质可证AO＝BO，可得AE＝BC，即可得四边形ABEC是矩形．

证明：（1）∵四边形ABCD是平行四边形，

∴AB∥CD，

∴∠BAO＝∠CEO，∠ABO＝∠ECO，

∵点O是边BC的中点，

∴BO＝CO，且∠BAO＝∠CEO，∠ABO＝∠ECO，

∴△ABO≌△ECO（AAS），

∴AO＝EO，且BO＝CO，

∴四边形ABEC是平行四边形；

（2）四边形ABEC是矩形，

理由如下：∵四边形ABCD是平行四边形，

∴∠ABC＝∠D＝50°，

∵∠AOC＝∠ABC+∠BAO＝100°，

∴∠ABC＝∠BAO＝50°，

∴AO＝BO，

∴AE＝BC，

∴ABEC是矩形．