题目内容
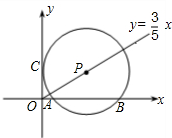 如图,P是射线y=
如图,P是射线y=| 3 | 5 |
分析:连接PC,过P作PD⊥x轴于E,利用勾股定理求出AE的长度,求出点A的坐标.
解答: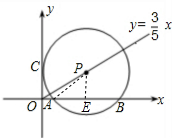 解:连接PC,过P作PD⊥x轴于E,
解:连接PC,过P作PD⊥x轴于E,
∵⊙P的半径为5,P是射线y=
x(x>0)上的一点,故P点坐标为(5,3),即OE=5,在Rt△APE中,AP=R=5,PE=3,故AE=
=
=4,故OA=OE-AE=5-4=1,故A点坐标是(1,0).
 解:连接PC,过P作PD⊥x轴于E,
解:连接PC,过P作PD⊥x轴于E,∵⊙P的半径为5,P是射线y=
| 3 |
| 5 |
| AP2-PE2 |
| 52-32 |
点评:此题把一次函数与圆相结合,考查了同学们综合运用所学知识的能力,是一道综合性较好的题目.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 24、如图,C是射线OE上的一动点,AB是过点C的弦,直线DA与OE的交点为D,现有三个论断:①DA是⊙O的切线;②DA=DC;③OD⊥OB.请你以其中的两个论断为条件,另一个论断为结论,用序号写出一个真命题,用“★★?★”表示.并给出证明.我的命题是:
24、如图,C是射线OE上的一动点,AB是过点C的弦,直线DA与OE的交点为D,现有三个论断:①DA是⊙O的切线;②DA=DC;③OD⊥OB.请你以其中的两个论断为条件,另一个论断为结论,用序号写出一个真命题,用“★★?★”表示.并给出证明.我的命题是: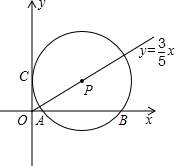 都在直线l上?若存在,请求出直线l的解析式;若不存在,请说明理由.
都在直线l上?若存在,请求出直线l的解析式;若不存在,请说明理由.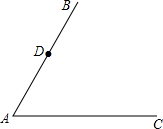 如图,D是射线AB上一点,过点D作DE∥AC,交∠BAC平分线于E,过点D作DF⊥AE,垂足为F.
如图,D是射线AB上一点,过点D作DE∥AC,交∠BAC平分线于E,过点D作DF⊥AE,垂足为F.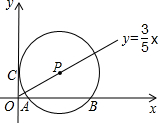 点都在直线l上?若存在,请求出直线l所对应的函数关系式;若不存在,请说明理由.
点都在直线l上?若存在,请求出直线l所对应的函数关系式;若不存在,请说明理由.