题目内容
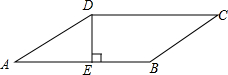如图，平行四边形ABCD的周长为22cm，DE⊥AB，垂足为E，cosA=| 4 |
| 5 |
| A、1cm | B、2cm |
| C、3cm | D、4cm |
考点：平行四边形的性质,解直角三角形
专题：
分析：由平行四边形的性质可知：AD+AB=11cm，利用已知条件可求出AD的长，进而得到AB的长，因为AE可求，所以BE的才可求出．
解答：解：∵平行四边形ABCD的周长为22cm，
∴AD+AB=11cm，
∵cosA=
，DE=3，
∴AE=4，AD=5，
∴AB=11-5=6，
∴BE=AB-AE=2cm，
故选B．
∴AD+AB=11cm，
∵cosA=
| 4 |
| 5 |
∴AE=4，AD=5，
∴AB=11-5=6，
∴BE=AB-AE=2cm，
故选B．
点评：本题考查了平行四边形的性质以及锐角三角函数，属于基础性题目．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
如图，在两个同心圆中，四条直径把大圆分成八等份，若往圆面投掷飞镖，则飞镖落在黑色区域的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图，△ABC的顶点坐标分别是A（3，6），B（1，3），C（4，2），如果将△ABC平移，使点A与点A′重合，得到△A′B′C′，那么点B的对应点B′的坐标是
如图，在山坡种树，已知∠A=30°，AC=3米，则相邻两株树的水平距离AB=用四舍五入法对下列各数取近似数：0.05678（精确到千分位）≈（ ）
| A、0.056 8 |
| B、0.057 |
| C、0.06 |
| D、0.1 |
下列因式分解错误的是（ ）
| A、a+ab-ac=a（b-c） |
| B、15a2+5a=5a（3a+1） |
| C、-x2+y2=（y+x）（y-x） |
| D、-a+4ax-4ax2=-a（2x-1）2 |