题目内容
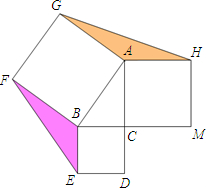 (2013•龙湾区一模)如图,以Rt△ABC的三边为边向外分别作正方形ACMH,正方形BCDE,正方形ABFG,连结EF,GH,已知∠ACB=90°,BC=t,AC=2-t (0<t<1).若图中阴影部分的面积和为0.84,则t=
(2013•龙湾区一模)如图,以Rt△ABC的三边为边向外分别作正方形ACMH,正方形BCDE,正方形ABFG,连结EF,GH,已知∠ACB=90°,BC=t,AC=2-t (0<t<1).若图中阴影部分的面积和为0.84,则t=0.6
0.6
.分析:过E做EI垂直FB的延长线与I,过H做HJ垂直GA的延长线与J,由相似三角形的判定方法可分别证明△ACB∽△EIB和△HAG∽△CAB,再有相似三角形的性质和三角形的内角公式以及已知条件即可求出t的值.
解答:解:过E做EI垂直FB的延长线与I,
∵∠ABC+∠FBE=180°,∠BID+∠FBE=180°
∴∠ABC=∠BID,
又∵∠ACB=∠EIB=90°
∴
=
,
∴AB•EI=BE•AC,
∴S△EDF=
EI•BF=
BE•AC=
(2t-t2),
过H做HJ垂直GA的延长线与J,
同理可证△HAJ∽△CAB,
∴
=
,
∴HJ•AC=AH•BC,
∴S△HAG=
HJ•AC=
AH•BC=(2t-t2),
∵S△EDF+S△HAG=0.84,
∴
(2t-t2)+
(2t-t2)=0.84,
解得t=0.6,
故答案为0.6.
∵∠ABC+∠FBE=180°,∠BID+∠FBE=180°
∴∠ABC=∠BID,
又∵∠ACB=∠EIB=90°
∴
| AB |
| BC |
| AC |
| EI |

∴AB•EI=BE•AC,
∴S△EDF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
过H做HJ垂直GA的延长线与J,
同理可证△HAJ∽△CAB,
∴
| AH |
| AC |
| HJ |
| BC |
∴HJ•AC=AH•BC,
∴S△HAG=
| 1 |
| 2 |
| 1 |
| 2 |
∵S△EDF+S△HAG=0.84,
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得t=0.6,
故答案为0.6.
点评:本题考查了正方形的性质,相似三角形的判定和性质以及一元二次方程的应用,题目的综合性强,难度较大.

练习册系列答案
相关题目
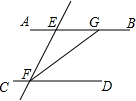 (2013•龙湾区一模)如图,已知AB∥CD,直线EF分别交AB,CD于点 E,F,FG平分∠EFD交AB于点G,若∠EFD=70°,则∠EGF的度数是( )
(2013•龙湾区一模)如图,已知AB∥CD,直线EF分别交AB,CD于点 E,F,FG平分∠EFD交AB于点G,若∠EFD=70°,则∠EGF的度数是( ) (2013•龙湾区一模)如图,△DEF是由△ABC通过平移得到,且点B,E,C,F在同一条直线上.若BF=14,EC=6.则BE的长度是( )
(2013•龙湾区一模)如图,△DEF是由△ABC通过平移得到,且点B,E,C,F在同一条直线上.若BF=14,EC=6.则BE的长度是( ) (2013•龙湾区一模)二次函数
(2013•龙湾区一模)二次函数