题目内容
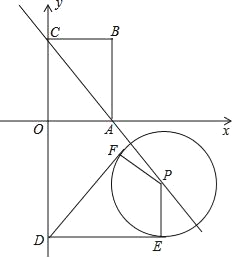
【题目】已知如图平面直角坐标系中,点O是坐标原点,矩形ABCO是顶点坐标分别为A(3,0)、B(3,4)、C(0,4).点D在y轴上,且点D的坐标为(0,﹣5),点P是直线AC上的一动点.
(1)当点P运动到线段AC的中点时,求直线DP的解析式(关系式);
(2)当点P沿直线AC移动时,过点D、P的直线与x轴交于点M.问在x轴的正半轴上是否存在使△DOM与△ABC相似的点M?若存在,请求出点M的坐标;若不存在,请说明理由;
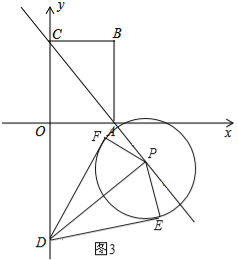
(3)当点P沿直线AC移动时,以点P为圆心、R(R>0)为半径长画圆.得到的圆称为动圆P.若设动圆P的半径长为![]() ,过点D作动圆P的两条切线与动圆P分别相切于点E、F.请探求在动圆P中是否存在面积最小的四边形DEPF?若存在,请求出最小面积S的值;若不存在,请说明理由.
,过点D作动圆P的两条切线与动圆P分别相切于点E、F.请探求在动圆P中是否存在面积最小的四边形DEPF?若存在,请求出最小面积S的值;若不存在,请说明理由.
【答案】(1)y=![]() x﹣5;(2)若△DOM与△CBA相似,则点M的坐标为(
x﹣5;(2)若△DOM与△CBA相似,则点M的坐标为(![]() ,0)或(
,0)或(![]() ,0);(3)
,0);(3)![]()
【解析】
试题(1)只需先求出AC中点P的坐标,然后用待定系数法即可求出直线DP的解析式.
(2)由于△DOM与△ABC相似,对应关系不确定,可分两种情况进行讨论,利用三角形相似求出OM的长,即可求出点M的坐标.
(3)易证S△PED=S△PFD.从而有S四边形DEPF=2S△PED=![]() DE.由∠DEP=90°得DE2=DP2﹣PE2=DP2﹣
DE.由∠DEP=90°得DE2=DP2﹣PE2=DP2﹣![]() .根据“点到直线之间,垂线段最短”可得:当DP⊥AC时,DP最短,此时DE也最短,对应的四边形DEPF的面积最小.借助于三角形相似,即可求出DP⊥AC时DP的值,就可求出四边形DEPF面积的最小值.
.根据“点到直线之间,垂线段最短”可得:当DP⊥AC时,DP最短,此时DE也最短,对应的四边形DEPF的面积最小.借助于三角形相似,即可求出DP⊥AC时DP的值,就可求出四边形DEPF面积的最小值.
解:(1)过点P作PH∥OA,交OC于点H,如图1所示.
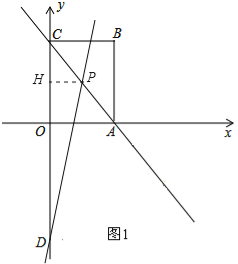
∵PH∥OA,
∴△CHP∽△COA.
∴![]() =
=![]() =
=![]() .
.
∵点P是AC中点,
∴CP=![]() CA.
CA.
∴HP=![]() OA,CH=
OA,CH=![]() CO.
CO.
∵A(3,0)、C(0,4),
∴OA=3,OC=4.
∴HP=![]() ,CH=2.
,CH=2.
∴OH=2.
∵PH∥OA,∠COA=90°,
∴∠CHP=∠COA=90°.
∴点P的坐标为(![]() ,2).
,2).
设直线DP的解析式为y=kx+b,
∵D(0,﹣5),P(![]() ,2)在直线DP上,
,2)在直线DP上,
∴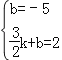
∴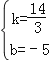
∴直线DP的解析式为y=![]() x﹣5.
x﹣5.
(2)①若△DOM∽△ABC,图2(1)所示,
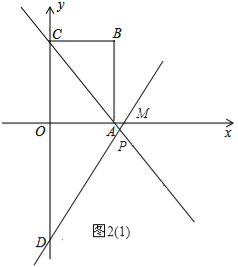
∵△DOM∽△ABC,
∴![]() =
=![]() .
.
∵点B坐标为(3,4),点D的坐标为(0.﹣5),
∴BC=3,AB=4,OD=5.
∴![]() =
=![]() .
.
∴OM=![]() .
.
∵点M在x轴的正半轴上,
∴点M的坐标为(![]() ,0)
,0)
②若△DOM∽△CBA,如图2(2)所示,
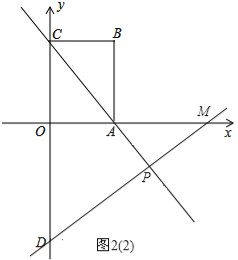
∵△DOM∽△CBA,
∴![]() =
=![]() .
.
∵BC=3,AB=4,OD=5,
∴![]() =
=![]() .
.
∴OM=![]() .
.
∵点M在x轴的正半轴上,
∴点M的坐标为(![]() ,0).
,0).
综上所述:若△DOM与△CBA相似,则点M的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
(3)∵OA=3,OC=4,∠AOC=90°,
∴AC=5.
∴PE=PF=![]() AC=
AC=![]() .
.
∵DE、DF都与⊙P相切,
∴DE=DF,∠DEP=∠DFP=90°.
∴S△PED=S△PFD.
∴S四边形DEPF=2S△PED
=2×![]() PEDE
PEDE
=PEDE
=![]() DE.
DE.
∵∠DEP=90°,
∴DE2=DP2﹣PE2.
=DP2﹣![]() .
.
根据“点到直线之间,垂线段最短”可得:
当DP⊥AC时,DP最短,
此时DE取到最小值,四边形DEPF的面积最小.
∵DP⊥AC,
∴∠DPC=90°.
∴∠AOC=∠DPC.
∵∠OCA=∠PCD,∠AOC=∠DPC,
∴△AOC∽△DPC.
∴![]() =
=![]() .
.
∵AO=3,AC=5,DC=4﹣(﹣5)=9,
∴![]() =
=![]() .
.
∴DP=![]() .
.
∴DE2=DP2﹣![]()
=(![]() )2﹣
)2﹣![]()
=![]() .
.
∴DE=![]() ,
,
∴S四边形DEPF=![]() DE
DE
=![]() .
.
∴四边形DEPF面积的最小值为![]() .
.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】甲、乙两名射击运动员进行射击比赛,两人在相同条件下,各射击10次,射击的成绩如图所示.根据统计图信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | 8 | b | 8 | s2 |
乙 | a | 7 | c | 0.6 |
(1)补充表格中a,b,c的值,并求甲的方差s2;
(2)运用表中的四个统计量,简要分析这两名运动员的射击成绩,若选派其中一名参赛,你认为应选哪名运动员?





