Question

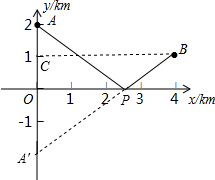
A，B两村在河边的同侧，以河边为x轴建立直角坐标系如图，则A，B两村对应的坐标分别为A（0，2），B（4，1），现要在河边P处修一个水泵站，分别向A，B两村送水，点P应选在何处，才可使所用的水管最短？求出所需水管的长度．

Answer 1

作点A关于x轴的对称轴A′，连接A′B交x轴于P，则此时P为所求，
过B作BC⊥y轴于C，
∵A（0，2），B（4，1），
∴A′的坐标是（0，-2），
∴A′C=3，BC=4，由勾股定理得：A′B=

32+42

=5，
即PA+PB=PA′+PB=A′B=5，
∴所需水管的长度是5．