题目内容
已知:如图,在正方形ABCD中,点E为AB的中点,点F为AD上一点,且AF=
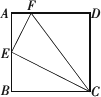
答案:
解析:
解析:
|
分析:只要说明△FEC的三边满足其中两边的平方和等于第三边的平方即可. 解:设正方形的边长为4a, 则AE=EB=2a,AF=a,FD=3a. 在Rt△AEF中,EF 2=a2+(2a)2=5a2;在Rt△BCE中,CE 2=(2a)2+(4a)2=20a2;在Rt△CDF中,CF2=(3a)2+(4a)2=25a2. 因为CF 2=CE2+EF2,所以△FEC是直角三角形.点评:在只知道边的条件下,若要判断一个三角形是不是直角三角形,常运用勾股定理的逆定理. |

练习册系列答案
相关题目
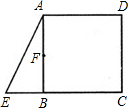 已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=
已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=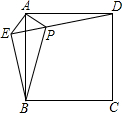 已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=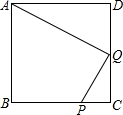 已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?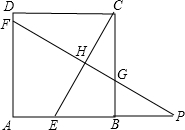 、CE、CB于点F、H、G,交AB的延长线于点P.
、CE、CB于点F、H、G,交AB的延长线于点P. 已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.
已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.