题目内容
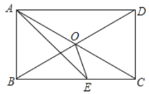
【题目】如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠OAE=15°,则∠AEO的度数为__________.
【答案】![]()
【解析】
根据矩形性质和角平分线的定义求证△ABO为等边三角形,从而得到∠ABO=60°,然后根据平行线的性质得出∠AEB=∠EAD=45°,从而得出BE=AB=BO,然后利用等腰三角形等边对等角的性质求得∠BEO=(180°-30°)÷2=75°,从而使问题得解.
解:∵四边形ABCD是矩形
∴OA=OB,∠BAD=∠ABC=90°,
又∵AE平分∠BAD
∴∠BAE=45°,
∴∠BAO=∠BAE +∠EAC =60°
∴△ABO为等边三角形
∴∠AOB=∠ABO=60°,
∴∠OBE=∠ABC-∠ABO=30°
∵AD//BC
∴∠AEB=∠EAD=45°
∴∠BAE=∠AEB
∴BE=AB=BO
∴∠BEO=(180°-30°)÷2=75°
∴∠AEO=∠BEO-∠AEB=30°
故答案为:30°.

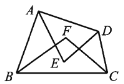
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )
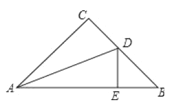
A. 4cm B. 6cm C. 8cm D. 10cm
【题目】近年来,“在初中数学教学候总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
n名学生对使用计算器影响计算能力的发展看法人数统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 40 | 60 | m |
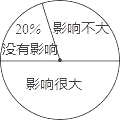
(1)求n的值;
(2)统计表中的m= ;
(3)估计该校1800名学生中认为“影响很大”的学生人数.