��Ŀ����
����������A��ȥ��B�У��ױ����������2��Сʱ������B�к�ͣ��һ��ʱ�䷵�أ��ҵ���B�к��������أ��׳��������ٶȶ�Ϊ40ǧ��/ʱ���ҳ��������ٶȶ�Ϊ20ǧ��/ʱ����ͼ��������A�е�·��S��ǧ�ף�����ʻʱ��t��Сʱ��֮��ĺ���ͼ������ͼ��ش��������⣺
��1��A��B���еľ������� ��ǧ�ף���B�к��� ��Сʱ�ҵ���B�У�
��2����׳�����ʱ��·��S��ǧ�ף���ʱ��t��Сʱ��֮��ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
��3����ֱ��д���׳���B�����ط����پ�����Сʱ�������15ǧ�ף�
��1��120��5��
��2��t��ȡֵ��ΧΪ��10��t��13��
��3��t=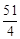 ��t=
��t=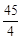 ��
��
���������������1������·��=�ٶȡ�ʱ���������ϵ�ü׳����ٶȡ��׳������ҵص�ʱ��ÿ���������صľ��룺
40��3=120km��
����ʱ��=·�̡��ٶȾͿ����������Ҫ��ʱ�䣺120��20��3+2=5Сʱ��
��2���ɣ�1���Ľ��ۿ������BD�Ľ���ʽ���ɴ���ϵ�����Ϳ���������ۡ�
��ͼ����AB���صľ�����120km��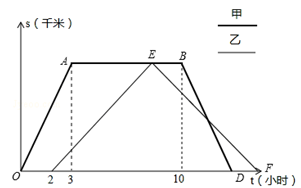
��A��3��120����B��10��120����D��13��0����
���߶�BD�Ľ���ʽΪS1=k1t+b1�������⣬�ã�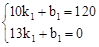 ����ã�
����ã�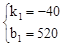 ��
��
��S1=��40t+520��
t��ȡֵ��ΧΪ��10��t��13��
��3�����ô���ϵ�������EF�Ľ���ʽ����������֮��ľ��빫ʽ�������������⼴�ɣ�
��EF�Ľ���ʽΪs2=k2t+b2�������⣬�ã�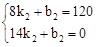 ����ã�
����ã�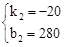 ����S2=��20t+280��
����S2=��20t+280��
����20t+280������40t+520��=15ʱ��t=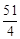 ������40t+520������20t+280��=15ʱ��t=
������40t+520������20t+280��=15ʱ��t=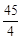 ��
��
��׳���B�����ط����پ���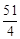 ��
��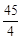 Сʱ�������15ǧ�ס���
Сʱ�������15ǧ�ס���

 �������ͬ������ϵ�д�
�������ͬ������ϵ�д�����ij�̳��мס���������Ʒ������ÿ������15Ԫ���ۼ�20Ԫ������ÿ������35Ԫ���ۼ�45Ԫ��
��1�����̼�ͬʱ�����ס���������Ʒ100���������Ʒ����x���������������Ʒ������Ϊy Ԫ��д��y��x�ĺ�����ϵʽ��
��2�����̼Ҽƻ����Ͷ��3000Ԫ���ڹ�����������Ʒ��100����������Ҫ�������ټ�������Ʒ����������Щ��Ʒ���̼ҿɻ�õ���������Ƕ���Ԫ��
��3������•һ���ڼ䣬�̼ҶԼס���������Ʒ���б��е��Żݻ��С�������̳�һ���Ը���324Ԫ���������Ʒ���̼ҿɻ�õ���С��������������Ƕ��٣�
| ����ǰһ���Թ����ܽ�� | �Żݴ�ʩ |
| ������400Ԫ | �ۼ۴���� |
| ����400Ԫ | �ۼ۴���� |





 λ�ڵڶ�����ͼ���ϣ���B1��B2������B2011�ں���
λ�ڵڶ�����ͼ���ϣ���B1��B2������B2011�ں��� ��
�� ������
������ ������������������
������������������
