题目内容
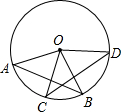如图，⊙O中，弦AB=CD．求证：∠AOC=∠BOD．
解：∵弦AB=CD（已知），∴
=
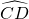；∴∠AOB=∠COD，
∴∠AOB-∠BOC=∠COD-∠BOC，
即∠AOC=∠BOD．
分析：因为弦AB=CD，所以
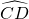=；然后根据圆心角、弧、弦的关系定理，可以证得∠AOC=∠BOD．点评：本题运用圆心角、弧、弦的关系定理解题，在同圆或等圆中，如果①两个圆心角，②两条弦，③两条弧，④两条弦的弦心距中，有任意一组量相等，其他各组量都相等．
练习册系列答案
相关题目
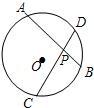10、如图，⊙O中，弦AB和CD相交于P，CP=2.5，PD=6，AB=8，那么以AP、PB的长为两根的一元二次方程是（ ）
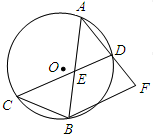如图，⊙O中，弦AB、CD相交于AB的中点E，连接AD并延长至点F，使DF=AD，连接BC、BF．
（2013•毕节地区）如图在⊙O中，弦AB=8，OC⊥AB，垂足为C，且OC=3，则⊙O的半径（ ）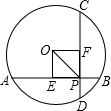
如图，⊙O中，弦AB，CD相交于P，且四边形OEPF是正方形，连接OP．若⊙O的半径为5cm，
如图，⊙O中，弦AB⊥CD于点E．若ON⊥BD于N，求证：ON=