题目内容
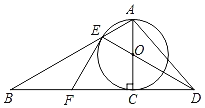
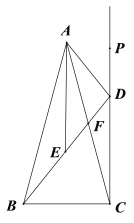
【题目】如图,在△ABC中,AB=AC,点F是AC边上的中点,DC⊥BC,与BF的延长线交于点D,AE平分∠BAC交BF于点E.
(1)求证:AE∥DC;
(2)若BD=8![]() ,求AD的长;
,求AD的长;
(3)若∠BAC=30°,AC=12,点P是射线CD上一点,求![]() CP+AP的最小值.
CP+AP的最小值.
【答案】(1)见解析;(2)4![]() ;(3)6
;(3)6![]()
【解析】
(1)根据等腰三角形的“三线合一”得AN⊥BC,再利用平行线的性质即可证明AE∥CD;
(2)连接CE,由等腰三角形的“三线合一”得出BN=CN,结合AN∥CD和CD⊥BC得到CE=![]() BD,再由AE∥CD和F为AC的中点证明△AEF≌△CDF,进而得到四边形AECD是平行四边形,所以AD=CE即可解答;
BD,再由AE∥CD和F为AC的中点证明△AEF≌△CDF,进而得到四边形AECD是平行四边形,所以AD=CE即可解答;
(3)在∠ACD外作∠DCG=30°,过CD上一点P1作P1M1⊥CG于M1,连接AP1,过点A作AM⊥CG交CD于点P.则P1M1=![]() CP1,PM=
CP1,PM=![]() CP,利用垂线段最短得知AM的长度为所求的最小值,进而在Rt△ACM中求得AM即可.
CP,利用垂线段最短得知AM的长度为所求的最小值,进而在Rt△ACM中求得AM即可.
证明:(1)延长AE交BC于点N.
∵AB=AC,AE平分∠BAC,∴AN⊥BC.
又∵CD⊥BC,
∴AE∥CD
(2)连接CE.
∵AB=AC,AE平分∠BAC,
∴BN=CN.
又∵AN∥CD,
∴BE=ED.
∵∠BCD=90°,
∴CE=![]() BD
BD
∵F是AC中点,
∴AF=CF.
∴AE∥CD.
∴∠EAC=∠DCA,∠AED=∠CDE.
∴△AEF≌△CDF(AAS).
∴EF=DF.
又AF=CF,
∴四边形AECD是平行四边形.
∴AD=CE=![]() BD,
BD,
∵BD=8![]() ,
,
∴AD=4![]()
(3)在∠ACD外作∠DCG=30°.
过CD上一点P1作P1M1⊥CG于M1,连接AP1,过点A作AM⊥CG交CD于点P.
在Rt△CP1M1和Rt△CPM中,∠DCG=30°,则P1M1=![]() CP1,PM=
CP1,PM=![]() CP.
CP.
∴![]() CP1+AP1=P1M1+AP1,
CP1+AP1=P1M1+AP1,![]() CP+AP=PM+AP=AM.
CP+AP=PM+AP=AM.
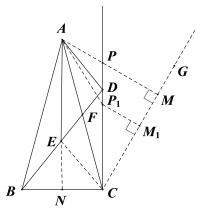
由“垂线段最短”可得P1M1+AP1≥AM,当A、P、M三点共线且AM⊥CM时,![]() CP+AP最小.
CP+AP最小.
∵∠BAC=30°,AE平分∠BAC,
∴∠EAC=15°.
∵AE∥CD,
∴∠DCA=∠EAC=15°.
∴∠ACM=∠ACD+∠DCM=45°.
在等腰Rt△ACM中,AC=12,
由勾股定理得2AM2=AC2=122
∴AM=6![]() .
.
∴![]() CP+AP的最小值是6
CP+AP的最小值是6![]() .
.