Question

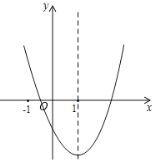
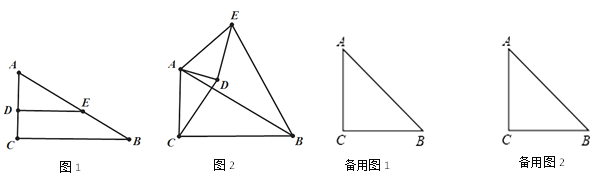
【题目】如图，抛物线y＝ax2+bx+c（a≠0）的顶点为C（2，﹣1），与x轴交于A，B两点，OA=3；

（1）求此抛物线的解析式；

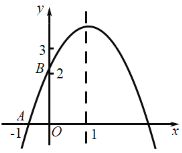
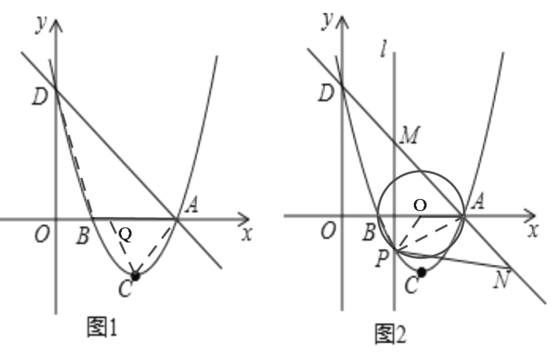
（2）如图1，一次函数y＝﹣x+3图象交x轴于点A，交y轴于点D，连结AC、BD，在x轴上有一点Q，使△AQC 与△ABD相似，求出点Q坐标；

（3）如图2，在直线y＝kx -1(k＞0）上是否存在唯一一点P，使得∠APB＝90°？若存在，请直接写出此时k的值；若不存在，请说明理由．

Answer 1

【答案】（1）y＝x2﹣4x+3；（2）Q点的坐标为（0，0）或（，0）；（3）存在，k=1，k=，k=．

【解析】

（1）由顶点坐标为C（2，﹣1）可得对称轴为x=2，然后再根据二次函数图像的对称性，确定A、B的坐标，然后使用待定系数法即可解答；

（2）先通过等腰三角形和相似三角形的性质得到∠CAQ＝∠DAB＝45°，然后分＝和＝两种情况解答即可；

（3）设P点坐标为（a，ka-1），以AB的中点O为圆心作⊙O，以AB为直径画圆恰好与直线y＝kx-1(k＞0）相切与P点，然后确定圆的半径长度，然后运用两点间距离公式列方程，最后根据条件即可确定k的取值．

解（1）∵函数图像的顶点坐标为C（2，﹣1）

∴对称轴为x=2

∵OA=3

∴B点的横坐标为:2-(3-2)=1,A点的横坐标为3

∴A(3,0),B(1,0)

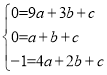∴解得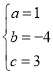

∴函数解析式为y＝x2﹣4x+3；

（2）如图：连接AC、QC、BD,

令x=0,则y＝﹣0+3=3，即点D坐标为（0,3）

∴OA=OD

∴∠DAB＝45°

要使△AQC∽△ADB，则∠CAQ＝∠DAB＝45°，

①当＝时，△AQC∽△ADB，即＝，解得AQ＝3，此时Q（0，0）；

②当＝时，△AQC∽△ABD，即＝，解得AQ＝，此时Q（，0）；

综上所述，Q点的坐标为（0，0）或（，0）；

（3）连接设P点坐标为（a，ka-1），以AB的中点O为圆心作⊙O，以AB为直径画圆恰好与直线y＝kx-1(k＞0）相切与P点，即AP⊥BP

∵A(3,0),B(1,0)

∴AO=BO=AB=1

∴即：（k-1）a2-（2k+2）a+1=0

∵在直线y＝kx-1(k＞0）上是否存在唯一一点P，使得∠APB＝90°

∴①当（k-1）a2-（2k+2）a+1=0为关于a的一元一次方程时，则k-1=1，即k=1；

②①当（k-1）a2-（2k+2）a+1=0为关于a的一元二次方程时，则：

（2k+2）2-4（k-1）=0解得：k=，k=；

综上，存在满足题意得k且取值为k=1，k=，k=．