Question

【题目】完成下列推理过程．
如图，DE∥BC，点D、A、E在同一条直线上，
求证：∠BAC+∠B+∠C=180°，
证明：∵DE∥BC
∴∠1=∠B，∠2=∠C
∵D、A、E在同一直线上（已知），
∴∠1+∠BAC+∠2=180°
∴∠BAC+∠B+∠C=180°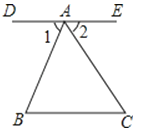

Answer 1

【答案】已知；两直线平行，内错角相等；补角的定义；等量代换
【解析】解：：∵DE∥BC（已知），
∴∠1=∠B，∠2=∠C（两直线平行，内错角相等）．
∵D、A、E在同一直线上（已知），
∴∠1+∠BAC+∠2=180°（补角的定义），
∴∠BAC+∠B+∠C=180°（等量代换）．
所以答案是：已知；两直线平行，内错角相等；平角定义；等量代换．
【考点精析】掌握平行线的性质是解答本题的根本，需要知道两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．