Question

【题目】如图，点A1（1， ）在直线l1：y= x上，过点A1作A1B1⊥l1交直线l2：y= x于点B1 ， A1B1为边在△OA1B1外侧作等边三角形A1B1C1 ， 再过点C1作A2B2⊥l1 ， 分别交直线l1和l2于A2 ， B2两点，以A2B2为边在△OA2B2外侧作等边三角形A2B2C2 ， …按此规律进行下去，则第n个等边三角形AnBnCn的面积为 ． （用含n的代数式表示）

Answer 1

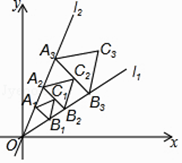
【答案】
【解析】解：∵点A1（1， ），
∴OA1=2．
∵直线l1：y= x，直线l2：y= x，
∴∠A1OB1=30°．
在Rt△OA1B1中，OA1=2，∠A1OB1=30°，∠OA1B1=90°，
∴A1B1= OB1 ，
∴A1B1= ．
∵△A1B1C1为等边三角形，
∴A1A2= A1B1=1，
∴OA2=3，A2B2= ．
同理，可得出：A3B3= ，A4B4= ，…，AnBn= ，
∴第n个等边三角形AnBnCn的面积为 × AnBn2= ．
所以答案是： ．