题目内容
【题目】如图,已知![]() 两点的坐标分别为
两点的坐标分别为![]() 将线段
将线段![]() 向右平移
向右平移![]() 个单位到线段
个单位到线段![]() 连接
连接![]() 得四边形
得四边形![]() .
.
(1)则点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ,
的坐标为 ,![]() ;
;
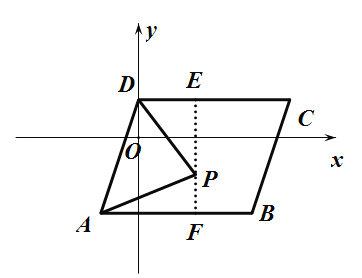
(2)如图①,若点![]() 为四边形
为四边形![]() 内的一点,且
内的一点,且![]() 求
求![]() 的值.
的值.

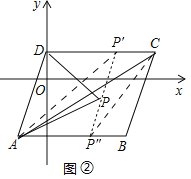
(3)如图②,若点![]() 为四边形
为四边形![]() 内的一点(包括边界).且
内的一点(包括边界).且![]() 当
当![]() 面积取最大值时,求此时对应的点
面积取最大值时,求此时对应的点![]() 的坐标和最大面积的值.[提示:
的坐标和最大面积的值.[提示:![]() ]
]
【答案】(1)![]() ,
,![]() ,12;(2)
,12;(2)![]() ;(3)当
;(3)当![]() 时,△PAC的面积最大,最大面积值为
时,△PAC的面积最大,最大面积值为![]() .
.
【解析】
(1)利用平移的性质,平行四边形的面积公式解决问题即可.
(2)如图①中,过点![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() .根据
.根据![]() ,构建方程解决问题即可.
,构建方程解决问题即可.
(3)作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() .利用面积法求出
.利用面积法求出![]() ,
,![]() 的坐标,求出△
的坐标,求出△![]() ,△
,△![]() 的面积比较即可判断.
的面积比较即可判断.
(1)![]() ,
,![]() ,线段
,线段![]() 向右平移4个单位得到线段
向右平移4个单位得到线段![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,根据平移的规律得:
是平行四边形,根据平移的规律得:![]() ,
,![]() ,
,
![]() ,
,
(2)如图①,过![]() 作
作![]() 轴
轴
则![]()
![]()
即![]()
解得![]()
(3)作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
同法可得![]() ,
,
![]() ,
,
![]() 当
当![]() ,
,![]() 时,
时,![]() 的面积最大,最大值为4.
的面积最大,最大值为4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目